题目内容
【题目】已知：边长为2的正方形OABC在平面直角坐标系中位于x轴上方，OA与x轴的正半轴的夹角为60°，则B点的坐标为_____.
【答案】
【解析】
根据“OA与x轴的正半轴的夹角为60°”可知OA与y轴正半轴的夹角为30°，根据正方形的边长为2，和三角函数值可将A点和C点坐标直接求出，将点B坐标设出，根据B到A和C和O的距离，列出方程组即可求出答案。
解：过点A作AM⊥y轴于点M
∵OA与x轴的正半轴的夹角为60°
∴OA与y轴正半轴的夹角为30°，OA=OC=2
∴AM=2xsin30°=1,OM=2xcos30°=
故点A的坐标为（1，）
过点C作CN⊥x轴于点N
∵OC与x轴的夹角为30°
∴CN=2xsin30°=1,ON=2xcos30°=
故点C的坐标为（
）
设点B坐标为（a,b）
过B作BE⊥x轴，交x轴于点E，过C作CD⊥BE，交BE于点D
∵OB=
，BD=b-1，CD=
∴
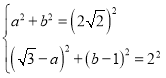
解得
∴点B的坐标为（
）
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
