题目内容
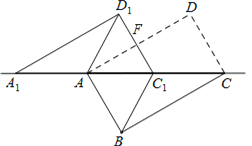
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,
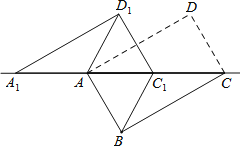
(1)求证:△A1AD1≌△CC1B;
(2)当CC1=1时,求证:四边形ABC1D1是菱形。
【答案】证明见解析
【解析】试题分析:(1)由矩形的性质及平移的性质易得∠A1=∠DAC,A1D1=AD,AA1=CC1,即可得到结论;
(2)由所给条件可证明△AC1B是等边三角形,即可得到ABC1D1是菱形.
试题解析:解:(1)∵四边形ABCD为矩形,
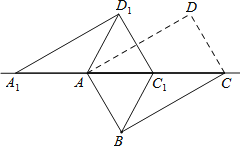
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠AA1 D1=∠DAC,A1D1=AD,AA1=CC1,
∴∠AA1 D1=∠ACB, BC= A1D1
在△A1AD1与△CC1B中,
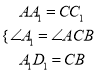 ,
,
∴△A1AD1≌△CC1B;
(2)证明∵∠ACB=30°,∴∠CAB=60°.
∵AB=1,∴AC=2.
∵CC1=1,∴AC1=1,∴△AC1B是等边三角形,.
∵AB=CD,CD=C1D1,∴AB= C1D1,∴四边形ABC1D1是平行四边形.
又AB=BC1,∴四边形ABC1D1是菱形.

练习册系列答案
相关题目