题目内容
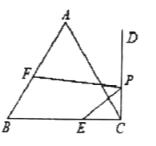
【题目】如图1,BD是矩形ABCD的对角线,∠ABD=30°,AD=1.将△BCD沿射线BD方向平移到△B′C′D′的位置,使B′为BD中点,连接AB′,C′D,AD′,BC′,如图2.
(1)求证:四边形AB′C′D是菱形;
(2)求四边形ABC′D′的周长.

图1 图2
【答案】(1)证明见解析;(2)四边形ABC′D′的周长为4![]() .
.
【解析】
(1)有一组邻边相等的平行四边形是菱形,据此进行证明即可。
(2)先判定四边形![]() 是菱形,再根据边长AB=
是菱形,再根据边长AB=![]() ,AD=
,AD=![]() ,即可得到四边形
,即可得到四边形![]() 的周长为
的周长为![]() .
.
(1)证明:∵BD是矩形ABCD的对角线,∠ABD=30°,
∴∠ADB=60°.
由平移可得B′C′=BC=AD,∠D′B′C′=∠DBC=∠ADB=60°.
∴AD∥B′C′.
∴四边形AB′C′D是平行四边形.
∵B′为BD中点,
∴Rt△ABD中,AB′=![]() BD=DB′.
BD=DB′.
又∵∠ADB=60°,
∴△ADB′是等边三角形.
∴AD=AB′.
∴四边形AB′C′D是菱形.
(2)由平移可得,AB=C′D′,∠ABD′=∠C′D′B=30°,
∴AB∥C′D′.
∴四边形ABC′D′是平行四边形.
由(1)可得,AC′⊥B′D,
∴四边形ABC′D′是菱形.
∵在Rt△DAB中,AB=![]() AD=
AD=![]() ,
,
∴四边形ABC′D′的周长为4![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目