题目内容
在平面直角坐标系xOy中,矩形ABCO的顶点A、C分别在y轴、x轴正半轴上,点P在AB上,PA=1,AO=2.经过原点的抛物线y=mx2-x+n的对称轴是直线x=2.
(1)求出该抛物线的解析式.
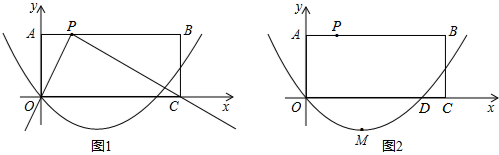
(2)如图1,将一块两直角边足够长的三角板的直角顶点放在P点处,两直角边恰好分别经过点O和C.现在利用图2进行如下探究:
①将三角板从图1中的位置开始,绕点P顺时针旋转,两直角边分别交OA、OC于点E、F,当点E和点A重合时停止旋转.请你观察、猜想,在这个过程中,
的值是否发生变化?若发生变化,说明理由;若不发生变化,求出
的值.
②设(1)中的抛物线与x轴的另一个交点为D,顶点为M,在①的旋转过程中,是否存在点F,使△DMF为等腰三角形?若不存在,请说明理由.
(1)求出该抛物线的解析式.
(2)如图1,将一块两直角边足够长的三角板的直角顶点放在P点处,两直角边恰好分别经过点O和C.现在利用图2进行如下探究:
①将三角板从图1中的位置开始,绕点P顺时针旋转,两直角边分别交OA、OC于点E、F,当点E和点A重合时停止旋转.请你观察、猜想,在这个过程中,
| PE |
| PF |
| PE |
| PF |
②设(1)中的抛物线与x轴的另一个交点为D,顶点为M,在①的旋转过程中,是否存在点F,使△DMF为等腰三角形?若不存在,请说明理由.

(1)∵抛物线y=mx2-x+n经过原点,∴n=0.
∵对称轴为直线x=2,∴-
=2,解得m=
.
∴抛物线的解析式为:y=
x2-x.
(2)①
的值不变.理由如下:
如答图1所示,过点P作PG⊥x轴于点G,则PG=AO=2.
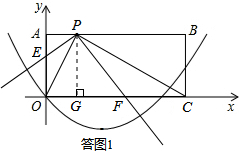
∵PE⊥PF,PA⊥PG,∴∠APE=∠GPF.
在Rt△PAE与Rt△PGF中,
∵∠APE=∠GPF,∠PAE=∠PGF=90°,
∴Rt△PAE∽Rt△PGF.
∴
=
=
.
②存在.
抛物线的解析式为:y=
x2-x,
令y=0,即
x2-x=0,解得:x=0或x=4,∴D(4,0).
又y=
x2-x=
(x-2)2-1,∴顶点M坐标为(2,-1).
若△DMF为等腰三角形,可能有三种情形:
(I)FM=FD.如答图2所示:
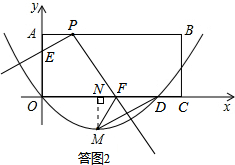
过点M作MN⊥x轴于点N,则MN=1,ND=2,MD=
=
=
.
设FM=FD=x,则NF=ND-FD=2-x.
在Rt△MNF中,由勾股定理得:NF2+MN2=MF2,
即:(2-x)2+1=x2,解得:x=
,
∴FD=
,OF=OD-FD=4-
=
,
∴F(
,0);
(II)若FD=DM.如答图3所示:
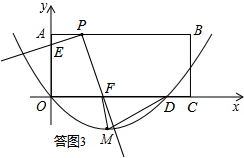
此时FD=DM=
,∴OF=OD-FD=4-
.
∴F(4-
,0);
(III)若FM=MD.
由抛物线对称性可知,此时点F与原点O重合.
而由题意可知,点E与点A重合后即停止运动,故点F不可能运动到原点O.
∴此种情形不存在.
综上所述,存在点F(
,0)或F(4-
,0),使△DMF为等腰三角形.
∵对称轴为直线x=2,∴-
| -1 |
| 2m |
| 1 |
| 4 |
∴抛物线的解析式为:y=
| 1 |
| 4 |
(2)①
| PE |
| PF |
如答图1所示,过点P作PG⊥x轴于点G,则PG=AO=2.

∵PE⊥PF,PA⊥PG,∴∠APE=∠GPF.
在Rt△PAE与Rt△PGF中,
∵∠APE=∠GPF,∠PAE=∠PGF=90°,
∴Rt△PAE∽Rt△PGF.
∴
| PE |
| PF |
| PA |
| PG |
| 1 |
| 2 |
②存在.
抛物线的解析式为:y=
| 1 |
| 4 |
令y=0,即
| 1 |
| 4 |
又y=
| 1 |
| 4 |
| 1 |
| 4 |
若△DMF为等腰三角形,可能有三种情形:
(I)FM=FD.如答图2所示:

过点M作MN⊥x轴于点N,则MN=1,ND=2,MD=
| MN2+ND2 |
| 12+22 |
| 5 |
设FM=FD=x,则NF=ND-FD=2-x.
在Rt△MNF中,由勾股定理得:NF2+MN2=MF2,
即:(2-x)2+1=x2,解得:x=
| 5 |
| 4 |
∴FD=
| 5 |
| 4 |
| 5 |
| 4 |
| 11 |
| 4 |
∴F(
| 11 |
| 4 |
(II)若FD=DM.如答图3所示:

此时FD=DM=
| 5 |
| 5 |
∴F(4-
| 5 |
(III)若FM=MD.
由抛物线对称性可知,此时点F与原点O重合.
而由题意可知,点E与点A重合后即停止运动,故点F不可能运动到原点O.
∴此种情形不存在.
综上所述,存在点F(
| 11 |
| 4 |
| 5 |

练习册系列答案
相关题目
 边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.
边上)的一个动点,点C在y轴上,抛物线y=ax2+bx+1以P为顶点.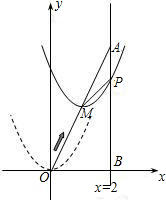
 1,0),顶点为B.
1,0),顶点为B.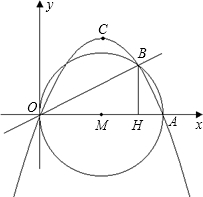 的⊙M上的两点,且tan∠AOB=
的⊙M上的两点,且tan∠AOB=
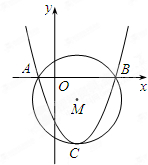
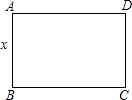 边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).
边AB的长为x(单位:米),矩形ABCD的面积为S(单位:平方米).