题目内容
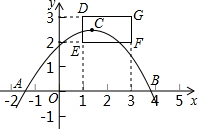
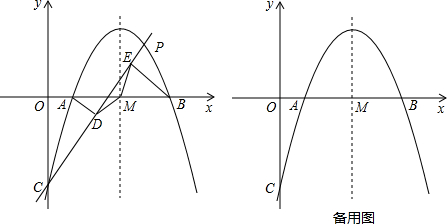
如图,在平面直角坐标系xOy中,二次函数y=-x2+bx+3的图象经过点A(-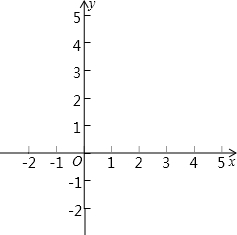 1,0),顶点为B.
1,0),顶点为B.
(1)求这个二次函数的解析式;
(2)若点C的坐标为(4,0),连接BC,过点A作AE⊥BC,垂足为点E.当点D在直线AE上,且满足DE=1时,求点D的坐标.
 1,0),顶点为B.
1,0),顶点为B.(1)求这个二次函数的解析式;
(2)若点C的坐标为(4,0),连接BC,过点A作AE⊥BC,垂足为点E.当点D在直线AE上,且满足DE=1时,求点D的坐标.
(1)∵二次函数y=-x2+bx+3的图象经过点A(-1,0),
∴0=-1-b+3,得b=2,(1分)
∴二次函数的解析式为y=-x2+2x+3;(2分)
(2)由(1)得这个二次函数图象顶点B的坐标为(1,4);(3分)
如图所示,过点B作BF⊥x轴,垂足为点F;
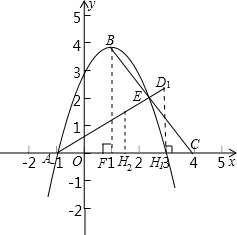 在Rt△BCF中,BF=4,CF=OC-OF=3,由勾股定理,得BC=5,
在Rt△BCF中,BF=4,CF=OC-OF=3,由勾股定理,得BC=5,
∴sin∠BCF=
;
∵AE⊥BC,垂足为点E,
∴∠AEC=90°;
在Rt△ACE中,sin∠ACE=
,
又AC=5,
可得
=
,
∴AE=4,由勾股定理得CE=3;
过点D作DH⊥x轴,垂足为点H;
由题意知,点H在y轴的右侧,易证△ADH∽△ACE;
设点D的坐标为(x,y),则AH=x+1,DH=y,(4分)
①若点D在AE的延长线上,则AD=5;
得
=
=
,
∴x=3,y=3,
所以点D的坐标为(3,3);(6分)
②若点D在线段AE上,则AD=3;
得
=
=
,
∴x=
,y=
,
所以点D的坐标为(
,
);
综上所述,点D的坐标为(3,3)或(
,
).
∴0=-1-b+3,得b=2,(1分)
∴二次函数的解析式为y=-x2+2x+3;(2分)
(2)由(1)得这个二次函数图象顶点B的坐标为(1,4);(3分)
如图所示,过点B作BF⊥x轴,垂足为点F;
 在Rt△BCF中,BF=4,CF=OC-OF=3,由勾股定理,得BC=5,
在Rt△BCF中,BF=4,CF=OC-OF=3,由勾股定理,得BC=5,∴sin∠BCF=
| 4 |
| 5 |
∵AE⊥BC,垂足为点E,
∴∠AEC=90°;
在Rt△ACE中,sin∠ACE=
| AE |
| AC |
又AC=5,
可得
| AE |
| 5 |
| 4 |
| 5 |
∴AE=4,由勾股定理得CE=3;
过点D作DH⊥x轴,垂足为点H;
由题意知,点H在y轴的右侧,易证△ADH∽△ACE;
设点D的坐标为(x,y),则AH=x+1,DH=y,(4分)
①若点D在AE的延长线上,则AD=5;
得
| x+1 |
| 4 |
| y |
| 3 |
| 5 |
| 5 |
∴x=3,y=3,
所以点D的坐标为(3,3);(6分)
②若点D在线段AE上,则AD=3;
得
| x+1 |
| 4 |
| y |
| 3 |
| 3 |
| 5 |
∴x=
| 7 |
| 5 |
| 9 |
| 5 |
所以点D的坐标为(
| 7 |
| 5 |
| 9 |
| 5 |
综上所述,点D的坐标为(3,3)或(
| 7 |
| 5 |
| 9 |
| 5 |

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
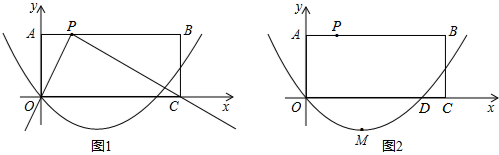

 行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.