��Ŀ����
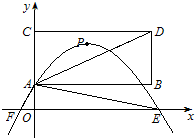
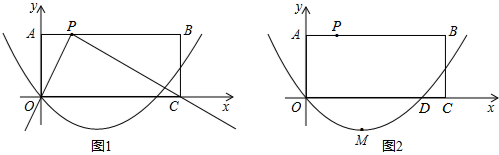
��ͼ����֪A��0��1����D��4��3����P����ADΪ�Խ��ߵľ���ABDC�ڲ������ڸ� ���ϣ���һ�����㣬��C��y���ϣ�������y=ax2+bx+1��PΪ���㣮
���ϣ���һ�����㣬��C��y���ϣ�������y=ax2+bx+1��PΪ���㣮
��1���ܷ��ж�������y=ax2+bx+1�Ŀ��ڷ�����˵�����ɣ�
��2����������y=ax2+bx+1��x���н���F��E��F��E����ࣩ����EAO���FAO�����֮��Ϊ3�����������������߶�AD��һ������ĺ�����Ϊ
����ʱ��ȷ��a��b��ֵ�����ܣ������a��b��ֵ�������ܣ���ȷ��a��b��ȡֵ��Χ���������ͼ�ν��������ο��ã�
 ���ϣ���һ�����㣬��C��y���ϣ�������y=ax2+bx+1��PΪ���㣮
���ϣ���һ�����㣬��C��y���ϣ�������y=ax2+bx+1��PΪ���㣮��1���ܷ��ж�������y=ax2+bx+1�Ŀ��ڷ�����˵�����ɣ�
��2����������y=ax2+bx+1��x���н���F��E��F��E����ࣩ����EAO���FAO�����֮��Ϊ3�����������������߶�AD��һ������ĺ�����Ϊ
| 7 |
| 2 |
��1�����ж������߿������£�
��y=ax2+bx+1������A��0��1����
���P��λ�ø��ڵ�A��˵����P���������ߵ���͵㣬
���P�������ߵ���ߵ㣮
��������y=ax2+bx+1�Ŀ������£�
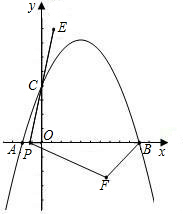
 ��2����ͼ������������x��Ľ�������ΪF��x1��0����E��x2��0����
��2����ͼ������������x��Ľ�������ΪF��x1��0����E��x2��0����
��x1��0��x2��0
S��AEO=
OE•OA=
x2��
S��AFO=
OF•OA=-
x1
��S��AEO-S��AFO=3
��
x2-��-
x1��=3����x1+x2=6
��x1+x2=
+
=-
��-
=6����b=-6a��
��һ���棬��ֱ��AD�Ľ���ʽΪy=kx+m��
���ѵ�A��0��1����D��4��3��������������ʽ��
�����
����y=
x+1
�������������߶�AD��һ������ĺ�����Ϊ
������������=
��
+1=
�ѵ㣨
��
�����������y=ax2+bx+1��
������49a+14b=7��
���ɢ٢���ɵķ������a=-
��b=
��
��y=ax2+bx+1������A��0��1����
���P��λ�ø��ڵ�A��˵����P���������ߵ���͵㣬
���P�������ߵ���ߵ㣮
��������y=ax2+bx+1�Ŀ������£�
 ��2����ͼ������������x��Ľ�������ΪF��x1��0����E��x2��0����
��2����ͼ������������x��Ľ�������ΪF��x1��0����E��x2��0������x1��0��x2��0
S��AEO=
| 1 |
| 2 |
| 1 |
| 2 |
S��AFO=
| 1 |
| 2 |
| 1 |
| 2 |
��S��AEO-S��AFO=3
��
| 1 |
| 2 |
| 1 |
| 2 |
��x1+x2=
-b+
| ||
| 2a |
-b-
| ||
| 2a |
| b |
| a |
��-
| b |
| a |
��һ���棬��ֱ��AD�Ľ���ʽΪy=kx+m��
���ѵ�A��0��1����D��4��3��������������ʽ��
|
|
| 1 |
| 2 |
�������������߶�AD��һ������ĺ�����Ϊ
| 7 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 11 |
| 4 |
�ѵ㣨
| 7 |
| 2 |
| 11 |
| 4 |
������49a+14b=7��
���ɢ٢���ɵķ������a=-
| 1 |
| 5 |
| 6 |
| 5 |

��ϰ��ϵ�д�
�����Ŀ
 ����0��2����
����0��2����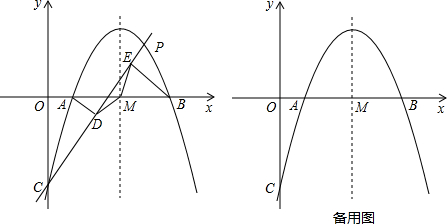
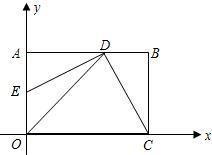
 A��D���㣬���������ཻ��B��1��m����C��2��2�����㣮
A��D���㣬���������ཻ��B��1��m����C��2��2�����㣮