题目内容
抛物线y=ax2+bx+3经过点A、B、C,已知A(-1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,延长DP交x轴于点F,M(m,0)是x轴上一动点,N是线段DF上一点,当△BDC的面积最大时,若∠MNC=90°,请直接写出实数m的取值范围.

(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,延长DP交x轴于点F,M(m,0)是x轴上一动点,N是线段DF上一点,当△BDC的面积最大时,若∠MNC=90°,请直接写出实数m的取值范围.

(1)由题意得:
,
解得:
,
故抛物线解析式为y=-x2+2x+3;
(2)令x=0,则y=3,即C(0,3).
设直线BC的解析式为y=kx+b′,
则
,解得:
,
故直线BC的解析式为y=-x+3.
设P(a,3-a),则D(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(3-a)=-a2+3a,
∴S△BDC=S△PDC+S△PDB=
PD•a+
PD•(3-a)=
PD•3=
(-a2+3a)=-
(a-
)2+
,
∴当a=
时,△BDC的面积最大,此时P(
,
);
(3)将x=
代入y=-x2+2x+3,得y=-(
)2+2×
+3=
,
∴点D的坐标为(
,
).
过点C作CG⊥DF,则CG=
.
①点N在DG上时,点N与点D重合时,点M的横坐标最大.
∵∠MNC=90°,∴CD2+DM2=CM2,
∵C(0,3),D(
,
),M(m,0),
∴(
-0)2+(
-3)2+(m-
)2+(0-
)2=(m-0)2+(0-3)2,
解得m=
.
∴点M的坐标为(
,0),
即m的最大值为
;
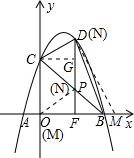 ②点N在线段GF上时,设GN=x,则NF=3-x,
②点N在线段GF上时,设GN=x,则NF=3-x,
∵∠MNC=90°,
∴∠CNG+∠MNF=90°,
又∵∠CNG+∠NCG=90°,
∴∠NCG=∠MNF,
又∵∠NGC=∠MFN=90°,
∴Rt△NCG∽△MNF,
∴
=
,即
=
,
整理得,MF=-
x2+2x=-
(x-
)2+
,
∴当x=
时(N与P重合),MF有最大值
,
此时M与O重合,
∴M的坐标为(0,0),
∴m的最小值为0,
故实数m的变化范围为0≤m≤
.
|
解得:
|
故抛物线解析式为y=-x2+2x+3;
(2)令x=0,则y=3,即C(0,3).
设直线BC的解析式为y=kx+b′,
则
|
|
故直线BC的解析式为y=-x+3.
设P(a,3-a),则D(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(3-a)=-a2+3a,
∴S△BDC=S△PDC+S△PDB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴当a=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)将x=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
∴点D的坐标为(
| 3 |
| 2 |
| 15 |
| 4 |
过点C作CG⊥DF,则CG=
| 3 |
| 2 |
①点N在DG上时,点N与点D重合时,点M的横坐标最大.
∵∠MNC=90°,∴CD2+DM2=CM2,
∵C(0,3),D(
| 3 |
| 2 |
| 15 |
| 4 |
∴(
| 3 |
| 2 |
| 15 |
| 4 |
| 3 |
| 2 |
| 15 |
| 4 |
解得m=
| 27 |
| 8 |
∴点M的坐标为(
| 27 |
| 8 |
即m的最大值为
| 27 |
| 8 |
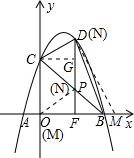 ②点N在线段GF上时,设GN=x,则NF=3-x,
②点N在线段GF上时,设GN=x,则NF=3-x,∵∠MNC=90°,
∴∠CNG+∠MNF=90°,
又∵∠CNG+∠NCG=90°,
∴∠NCG=∠MNF,
又∵∠NGC=∠MFN=90°,
∴Rt△NCG∽△MNF,
∴
| CG |
| NF |
| GN |
| MF |
| ||
| 3-x |
| x |
| MF |
整理得,MF=-
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴当x=
| 3 |
| 2 |
| 3 |
| 2 |
此时M与O重合,
∴M的坐标为(0,0),
∴m的最小值为0,
故实数m的变化范围为0≤m≤
| 27 |
| 8 |

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
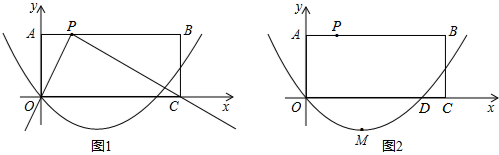

 行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.

