Question

如图，在直角坐标系中，O是坐标原点，A（3，0）、B（m，

6

5

）是以OA为直径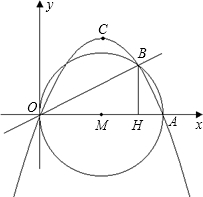的⊙M上的两点，且tan∠AOB=

1

2

，BH⊥x轴，垂足为H
（1）求H点的坐标；
（2）求图象经过A、B、O三点的二次函数的解析式；
（3）设点C为（2）中的二次函数图象的顶点，问经过B、C两点的直线是否与⊙M相切，请说明理由．
注：抛物线y=ax²+bx+c（c≠0）的顶点为(-

b

2a

，

4ac-b2

4a

)．

Answer 1

（1）∵tan∠AOB=

1

2

，∴

BH

OH

=

1

2

，
∵B（m，

6

5

），∴OH=

12

5

；
∴H点的坐标（

12

5

，0）；

（2）设二次函数的解析式为y=ax²+bx+c，
∴B（

12

5

，

6

5

），
将A、B、O三点坐标代入得，

144 25 a+ 12 5 b+c= 6 5 9a+3b+c=0 c=0

，
解得

a=- 5 6 b= 5 2 c=0

，
∴二次函数的解析式为y=-

5

6

x²+

5

2

x；

（3）∵抛物线y=ax²+bx+c（c≠0）的顶点为(-

b

2a

，

4ac-b2

4a

)．
∴C（

3

2

，

15

8

），
设直线BC的解析式为y=kx+b，将点B、C坐标代入得，

12 5 k+b= 6 5 3 2 k+b= 15 8

，
解得k=-

3

4

，b=3，
∴直线BC的解析式为y=-

3

4

x+3，
∵M（1.5，0），
∴直线BM的解析式为y=-

4

3

x-2，
∴BM⊥BC，
∴经过B、C两点的直线与⊙M相切．