题目内容
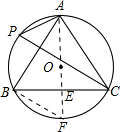
如图所示，已知AB=AC，∠APC=60°．
（1）求证：△ABC是等边三角形；
（2）若BC=4
，求⊙O的面积．
（1）求证：△ABC是等边三角形；
（2）若BC=4
| 3 |
证明：（1）在⊙O中，∠ABC=∠APC=60°，
∵AB=AC，
∴△ABC为等边三角形．
（2）连接AO并延长交圆O于F，交BC于E，
如图所示，圆O为等边△ABC的外接圆，
∴AE⊥BC，BE=CE=2
，
在Rt△ABE中，AE=
=6，
在Rt△ABF中，AE⊥BC，
∴∠ABF=∠AEB=90°，
又∵∠BAF=∠EAB，
∴△BAE∽△FAB，
∴
=
∴AF=
=8，
∴半径为4，
面积S=πr2=16π．
∵AB=AC，
∴△ABC为等边三角形．
（2）连接AO并延长交圆O于F，交BC于E，
如图所示，圆O为等边△ABC的外接圆，
∴AE⊥BC，BE=CE=2
| 3 |
在Rt△ABE中，AE=
| AB2-BE2 |
在Rt△ABF中，AE⊥BC，
∴∠ABF=∠AEB=90°，
又∵∠BAF=∠EAB，
∴△BAE∽△FAB，
∴
| AB |
| AF |
| AE |
| AB |
∴AF=
| AB2 |
| AE |
∴半径为4，
面积S=πr2=16π．
练习册系列答案
相关题目
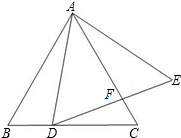
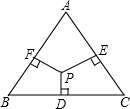
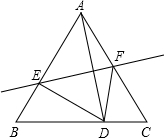作AD的垂直平分线分别与边AB、AC交于点E、F．