题目内容
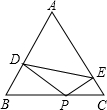
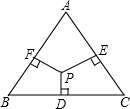
如图所示,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF等于( )
A.
| B.2
| C.4
| D.无法确定 |

连接AP、BP、CP,设等边三角形的高为h
∵正三角形ABC边长为2
∴h=
=
∵S△BPC=
BC•PD
S△APC=
AC•PE
S△APB=
AB•PF
∴S△ABC=
BC•PD+
AC•PE+
AB•PF
∵AB=BC=AC
∴S△ABC=
BC•(PD+PE+PF)=
BC•h
∴PD+PF+PE=h=
故选A.
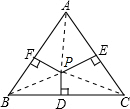
∵正三角形ABC边长为2
∴h=
| 22-12 |
| 3 |
∵S△BPC=
| 1 |
| 2 |
S△APC=
| 1 |
| 2 |
S△APB=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=BC=AC
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴PD+PF+PE=h=
| 3 |
故选A.


练习册系列答案
相关题目