��Ŀ����
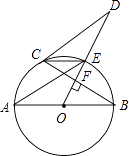
����Ŀ����֪A��B��C��D��E��F�ֱ��ǡ�O�ϵ����ȷֵ㣬��O�İ뾶��100���������������ͨ�ĵ�·����ͼ��ʵ�߲���Ϊ��·���������������ַ���������һ����ͼ1�������߶γ��Ⱦ���ȣ���ͼ�е�·��Ϊl1������������ͼ2��AQ=BG=CH=DM=EN=FP����G��H��M��N��P��Q�ֱ����߶�AQ��BG��CH��DM��EN��FP���е㣬������GHMNPQ����OΪ���ĵ��������Σ���ͼ�е�·��Ϊl2����l1= ��l2= �� 
���𰸡�![]() ��
��![]()
���������⣺��ͼ1������OA��OB������M��MG![]() OA�ڵ�G��
OA�ڵ�G��
��A��B��C��D��E��F�ֱ��ǡ�O�ϵ����ȷֵ㣬��O�İ뾶��100��
��![]() AOB=60
AOB=60![]() ��
��
�߸����߶γ��Ⱦ���ȣ�
��![]() AOM=30
AOM=30![]() ��
��
��Rt![]() OMG����OG=
OMG����OG=![]() OA=50����OM=
OA=50����OM=![]() ��
��
��l1=![]()
![]() 9=
9=![]() .
.
��ͼ2������OB������O��OR��BF�ڵ�R��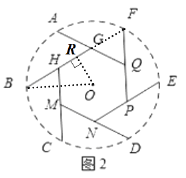
��AQ=BG=CH=DM=EN=FP����G��H��M��N��P��Q�ֱ����߶�AQ��BG��CH��DM��EN��FP���е㣬������GHMNPQ����OΪ���ĵ��������Σ����ӳ�BG�����F�غϣ���H�͵�G��BF�����ȷֵ�.
��Rt �� OBR����![]() OBR=30 �� ��OB=100����BR=
OBR=30 �� ��OB=100����BR=![]() ����BF=
����BF=![]() ��
��
��BG=![]() BF=
BF=![]() ��
��
��l2=![]()
![]() 6=
6=![]() .
.
���Դ��ǣ�![]() ��
��![]() .
.
�����㾫��������������ε����ʺ�������κ�Բ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪������ζ�����Գ�ͼ�Σ�һ����n���ι���n���Գ��ᣬÿ���Գ��ᶼͨ����n���ε�����;������ε����ı���Ϊż����������������ĶԳ�ͼ�Σ����ĶԳ�������������ε����ģ�Բ���ڽ��ı��εĶԽǻ����������κ�һ����Ƕ����������ڶԽǣ�Բ�������ı��ε�����Աߵĺ���ȣ�

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�