Question

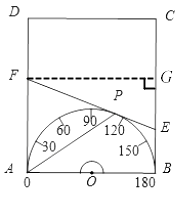
【题目】如图，矩形ABCD的边AB=4，且BC＞AB，一个量角器如图所示放置，其中零刻度（即半圆O的直径）与边AB重合，点A处是0刻度，点B处是180刻度，点P是量角器的半圆弧上一动点，过点P作半圆的切线，设点P的刻度数为m，过点P的切线交线段BC与线段AD于点E，F．

（1）设∠PAB=n．
①如图1，当m=114°时，n=；
②直接写出n与m的关系式：；
（2）试说明AF·BE是否是一个定值，若是，请求出它的值；若不是，请说明理由；
（3）当EF= 时，求点P的刻度数m的值．

Answer 1

【答案】
（1）33°；解：∵OA=OP
∴∠APO=∠PAO=n
又∵∠AOP=m
∴2n+m=180°
∴n=90°-
（2）

解：AF·BE是一个定值，理由如下：

过点F作FG⊥BC于G．

∵AF，EF，BE是⊙O的切线

∴AF=PF，PE=BE， FE=PF+PE=AF+BE

在Rt△FGE中，GE2+GF2=FE2

∴（AF-BE）2+42=(AF+BE)2

∴AF·BE=4

（3）

解：设AF=x，BE=y

∴xy=4，EF=AF+BE=x+y=

∴（ -x）·x=4，即x 2- x+4=0

解得：x1=2 ，x2=

(ⅰ)当x1=2 时，可求得FO=4

∴AO= FO，∴∠AFO=30°，∴∠AOF=60°

∴∠AOP=2∠AOF=120°

即m=120°．

(ⅱ)当x2= 时，可求得FO=

∴∠AOF=30°，∴∠AOP=60°

即m=60°．

综上可得，点P对应的刻度m的值为120°或60°．

答：点P的刻度数m的值为120°或60°．

【解析】（1）连接OP，AOP是等腰三角形，利用等腰三角形的性质求解即可.
（2）过点F作FG⊥BC于G，利用切线长定理及勾股定理列等式，化简即可得出AF·BE=4.
（3）充分利用第（2）问的结论，注意分(ⅰ)当x1= 时和(ⅱ)当x2=时两种情况讨论.
【考点精析】认真审题，首先需要了解切线长定理(从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角)，还要掌握等腰三角形的性质(等腰三角形的两个底角相等（简称：等边对等角）)的相关知识才是答题的关键．