题目内容
【题目】阅读下列两则材料,回答问题:
材料一:平面直角坐标系中,对点A(x1,y1),B(x2,y2)定义一种新的运算:AB=x1x2+y1y2.
例如:若A(1,2),B(3,4),则AB=1×3+2×4=11
材料二:平面直角坐标系中,过横坐标不同的两点A(x1,y1),B(x2,y2)的直线的斜率为kAB=![]() .由此可以发现若kAB=
.由此可以发现若kAB=![]() =1,则有y1-y2=x1-x2,即x1-y1=x2-y2.反之,若x1,x2,y1,y2满足关系式x1-y1=x2-y2,则有y1-y2=x1-x2,那么kAB=
=1,则有y1-y2=x1-x2,即x1-y1=x2-y2.反之,若x1,x2,y1,y2满足关系式x1-y1=x2-y2,则有y1-y2=x1-x2,那么kAB=![]() ═1.
═1.
(1)已知点M(-4,6),N(3,2),则MN=______,若点A,B的坐标分别为(x1,y1),(x2,y2)(x1≠x2),且满足关系式x1+y1=x2+y2,那么kAB=______;
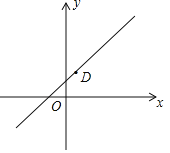
(2)横坐标互不相同的三个点C,D,E满足CD=DE,且D点的坐标为(2,2),过点D作DF∥y轴,交直线CE于点F,若DF=8,请结合图象,求直线CE与坐标轴围成的三角形的面积.
【答案】(1)0,-1;(2)8或72.
【解析】
(1)根据材料一和材料二计算即可;
(2)由CD=DE,且D点的坐标为(2,2),得出x1+y1=x2+y2,即可得出直线CE的斜率为kCE=-1,从而得出直线CE与坐标轴围成的三角形是等腰直角三角形,然后根据图象即可求得.
解:(1)根据新的运算,MN=-4×3+6×2=0;
∵点A,B的坐标分别为(x1,y1),(x2,y2)(x1≠x2),且满足关系式x1+y1=x2+y2,
∴y1-y2=-(x1-x2),
∴kAB=![]() =-1;
=-1;
故答案为0,-1;
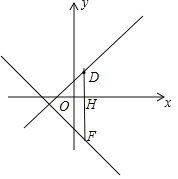
(2)设点C,E的坐标分别为(x1,y1),(x2,y2)(x1≠x2),
∵CD=DE,且D点的坐标为(2,2),
∴2x1+2y1=2x2+2y2,即x1+y1=x2+y2,
由(1)可知:直线CE的斜率为kCE=-1,
如图所示,则直线CE与坐标轴围成的三角形是等腰直角三角形,
∵DF=8,
∴围成的三角形的直角边的长为4或12,
∴直线CE与坐标轴围成的三角形的面积为8或72.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 | 成活数 | 成活率 | 移植棵数 | 成活数 | 成活率 |
50 | 47 |
| 1500 | 1335 |
|
270 | 235 |
| 3500 | 3203 |
|
400 | 369 |
| 7000 | 6335 |
|
750 | 662 |
| 14000 | 12628 |
|
下面有四个推断:
①当移植的树数是1500时,表格记录成活数是1335,所以这种树苗成活的概率是![]() ;
;
②随着移植棵数的增加,树苗成活的频率总在![]() 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是
附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是![]() ;
;
③若小张移植10000棵这种树苗,则可能成活9000棵;
④若小张移植20000棵这种树苗,则一定成活18000棵.
其中合理的是![]()
![]()
A. ①③B. ①④C. ②③D. ②④
【题目】近期,第八届“重庆车博会“在会展中心盛大开幕,某汽车公司推出降价促销活动,销售员小王提前做了市场调查,发现车辆的销量y(辆)与售价(万元/辆)存在如下表所示的一次函数关系:
售价x(万元/辆) | … | 20 | 19.8 | 19.6 | 19.4 | 19.2 | 19 | … |
销量y(辆) | … | 5 | 6 | 7 | 8 | 9 | 10 | … |
(1)求y与x之间的函数关系式;
(2)若每辆车的成本为11万元,在每辆车售价不低于15万元的前提下,每辆车的售价定为多少万元时,汽车公司获得的总利润W(万元)有最大值?最大值是多少?