题目内容
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
（1）求证：直线l与该抛物线总有两个交点；
（2）设直线l与该抛物线两交点为A，B，O为原点，当k=-2时，求△OAB的面积.
【答案】（1）证明见解析；（2）
.
【解析】（1）联立两解析式，根据判别式即可求证；
（2）画出图象，求出A、B的坐标，再求出直线y=-2x+1与x轴的交点C，然后利用三角形的面积公式即可求出答案．
（1）联立
化简可得：x2-（4+k）x-1=0，
∴△=（4+k）2+4＞0，
故直线l与该抛物线总有两个交点；
（2）当k=-2时，
∴y=-2x+1
过点A作AF⊥x轴于F，过点B作BE⊥x轴于E，
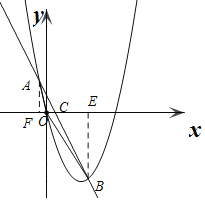
∴联立
解得：
或
∴A（1-，2-1），B（1+，-1-2）
∴AF=2-1，BE=1+2
易求得：直线y=-2x+1与x轴的交点C为（
，0）
∴OC=1
∴S△AOB=S△AOC+S△BOC
=OCAF+OCBE
=OC（AF+BE）
=×（2-1+1+2）
=2.
练习册系列答案
名校课堂系列答案
相关题目
