题目内容
【题目】已知边长为5的菱形ABCD中,对角线AC长为6,点E在对角线BD上且tan∠EAC=![]() ,则BE的长为_____.
,则BE的长为_____.
【答案】3或5
【解析】
菱形ABCD中,边长为5,对角线AC长为6,由菱形的性质及勾股定理可得AC⊥BD,BO=4,分当点E在对角线交点左侧时(如图1)和当点E在对角线交点左侧时(如图2)两种情况求BE得长即可.
当点E在对角线交点左侧时,如图1所示:
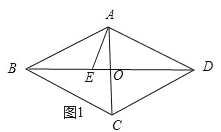
∵菱形ABCD中,边长为5,对角线AC长为6,
∴AC⊥BD,BO=![]() =4,
=4,
∵tan∠EAC=![]() ,
,
解得:OE=1,
∴BE=BO﹣OE=4﹣1=3,
当点E在对角线交点左侧时,如图2所示:
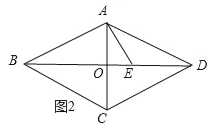
∵菱形ABCD中,边长为5,对角线AC长为6,
∴AC⊥BD,BO=![]() =4,
=4,
∵tan∠EAC=![]() ,
,
解得:OE=1,
∴BE=BO﹣OE=4+1=5,
故答案为:3或5.

练习册系列答案
相关题目