题目内容
【题目】已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
(1)观察图形,猜想BD与⊙O的位置关系;
(2)证明第(1)题的猜想
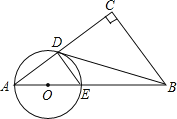
【答案】(1)相切;(2)详见解析.
【解析】
(1)观察图形,可得BD与⊙O的位置关系:相切;
(2)首先连接OD,由AE是⊙O的直径,在Rt△ABC中,∠C=90°,易证得DE∥BC,又由∠CBD=∠A,可证得∠ODE+∠EDB=90°,即可证得结论.
(1)解:相切.
(2)证明:连接OD,
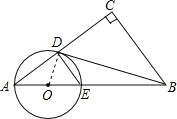
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠A+∠AED=90°,
∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
∴∠EDB=∠CBD,
∵∠CBD=∠A,
∴∠EDB=∠A,
∵OD=OE,
∴∠ODE=∠OED,
∴∠ODE+∠EDB=90°,
即OD⊥BD,
∴BD与⊙O的位置关系是相切.

练习册系列答案
相关题目