题目内容
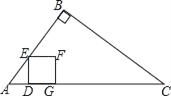
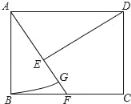
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
(1)求证:DE=AB;
(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据矩形的性质得出∠B=90°,AD=BC,AD∥BC,求出∠DAE=∠AFB,∠AED=90°=∠B,根据AAS推出△ABF≌△DEA即可;
(2)根据勾股定理求出AB,解直角三角形求出∠BAF,根据全等三角形的性质得出DE=AB=![]() ,∠BAF=30°,根据扇形的面积公式求出即可.
,∠BAF=30°,根据扇形的面积公式求出即可.
(1)∵四边形ABCD是矩形,
∴∠B=90°,AD=BC,AD∥BC,
∴∠DAE=∠AFB,
∵DE⊥AF,
∴∠AED=90°=∠B,
在△ABF和△DEA中
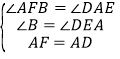 ,
,
∴△ABF≌△DEA(AAS),
∴DE=AB;
(2)∵BF=FC=1
∴BC=BF+FC=2
由(1)得:△ABF≌△DEA
∴AD=AF,
∵BC=AD,
∴AF =BC=2,
∵BF=1,∠ABF=90°,
∴由勾股定理得:AB=![]()
∴sin∠BAF=![]() ,
,
∴∠BAF=30°
∴扇形ABG的面积=![]()

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目