题目内容
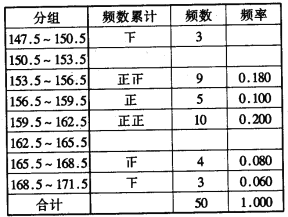
【题目】如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD＝6，阴影部分图形的面积为（ ）
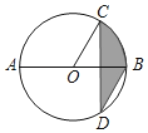
A. 4πB. 3πC. 2πD. π
【答案】C
【解析】
先求出△BOC是等边三角形，再根据垂径定理及圆周角定理得到∠CBO＝∠BOD，由S△BCD＝S△BCO将阴影部分面积转化为S扇形OBC，代入数值求解即可.
解：连接BC，OD，设CD交AB于E．
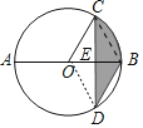
∵∠BOC＝2∠CDB，∠CDB＝30°，
∴∠COB＝60°，
∵OC＝OB，
∴△BOC是等边三角形，
∴∠CBO＝60°，
∵CD⊥AB，CD＝6，
∴
＝
，CE＝ED＝3，
∴∠BOC＝∠BOD＝60°，EO＝
，OC＝2，
∴∠CBO＝∠BOD，
∴BC∥OD，
∴S△BCD＝S△BCO，
∴S阴＝S扇形OBC＝
＝2π．
故选：C．
练习册系列答案
相关题目
