Question

【题目】在Rt△ABC 中，∠C=90°，BC=3，AC=4．现在要将交ABC 扩充成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后等腰三角形的周长．

赵佳同学是这样操作的：如图 1 所示，延长BC 到点 D，使CD=BC，连接AD．所以，△ADB 为符合条件的三角形．则此时△ADB的周长为____________．

请你在图2、图3中再设计两种扩充方案，并直接写出扩充后等腰三角形的周长．

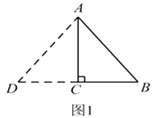
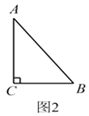
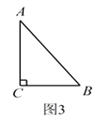
图2的周长：______________；图3的周长：______________.

Answer 1

【答案】 16 10+2

【解析】试题分析：利用勾股定理可求出AB的长进而得出△ADB的周长；再根据题目要求扩充成AC为直角边的直角三角形，利用AB=BD，AD=BD，分别得出答案．

试题解析：

∵在Rt△ABC中，∠C=90°，BC=3，AC=4，CD=BC，
∴AB=，则AD=AB=5，
故此时△ADB的周长为：5+5+6=16；
如图2所示：AD=BD时，设DC=x，则AD=x+3，
在Rt△ADC中，
（x+3）2=x2+42，
解得：x=，
故AD=3+= ，
则此时△ADB的周长为： ++5= ；
如图3所示：AB=BD时，在Rt△ADC中，
AD=，
则此时△ADB的周长为： +5+5=10+．
故答案为（1）16；（2）10+2， ．