题目内容
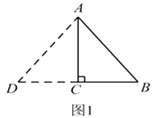
【题目】如图,在△ABC中,D为BC的中点,E,F分别是AB,AC上的点,且DE⊥DF.
求证:BE+CF>EF. 
【答案】证明:如图,延长ED至点M,使DM=ED,连接MC,MF,则EF=FM .
∵BD=CD,ED=DM,∠EDB=∠CDM,
∴△BDE≌△CDM(SAS).
∴BE=CM.
∵CF+CM>MF,
∴BE+CF>EF.
【解析】延长ED至点M,使DM=ED,连接MC,MF,根据中垂线的性质得出 ：EF=FM ,然后利用SAS判断出△BDE≌△CDM ，根据全等三角形的对应边相等得出BE=CM ，根据三角形三边之间的关系得出CF+CM>MF,然后等量代换得出BE+CF>EF. 。
【考点精析】认真审题，首先需要了解三角形三边关系(三角形两边之和大于第三边；三角形两边之差小于第三边；不符合定理的三条线段，不能组成三角形的三边)，还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键．
练习册系列答案
相关题目
