��Ŀ����
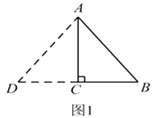
����Ŀ��ij��ѧ������Ȥ�С����Χ��һ����������������һ�߿�ǽ�����������ܳ�Ϊ30�����Χ�ɣ���֪ǽ��Ϊ18��(����ͼ��ʾ)�������������ֱ��ǽ��һ�߳�Ϊx�ף�
�������������Ϊ72ƽ���ף���x��
����ƽ����ǽ��һ�߳���С��8�ף������������������ֵ����Сֵ������У�������ֵ����Сֵ�����û�У���˵�����ɣ�
�ǵ���������������С��100ƽ����ʱ��ֱ��д��x��ȡֵ��Χ��

���𰸡���1��x1��3��x2��12��2���ٵ�x��![]() ʱ�� S�����
ʱ�� S�����![]() �� �ڵ�x��11ʱ�� S��С��11��(30��22)��88����3��5��x��10��
�� �ڵ�x��11ʱ�� S��С��11��(30��22)��88����3��5��x��10��
����������1����������÷�����⼴�ɣ���2�������������Ϊy����������õ����κ�������ʽy=x��30-2x��=-2x2+30x�����ݶ��κ�����������⼴�ɣ���3��������ò���ʽ�����ɵõ�����.
�⣺(1)������ǽƽ�е�һ�߳�Ϊ(30��2x)�ף���������з���
x(30��2x)��72����x2��15x��36��0��
���x1��3��x2��12��
(2)�����⣬��8��30��2x��18�����6��x��11��
���S��x(30��2x)����2(x��![]() )2��
)2��![]() (6��x��11)��
(6��x��11)��
�ٵ�x��![]() ʱ��S�����ֵ��S�����
ʱ��S�����ֵ��S�����![]() ��
��
�ڵ�x��11ʱ��S����Сֵ��S��С��11��(30��22)��88��
(3)��x(30��2x)��100����x2��15x��50��0��
���x1��5��x2��1
��x��ȡֵ��Χ��5��x��10��