题目内容
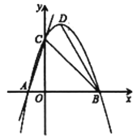
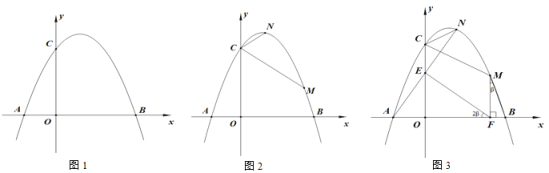
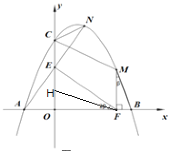
【题目】如图1,抛物线y= -![]() x2+bx+c与x轴负半轴交于A点,与x轴正半轴交于B点,与y轴正半轴交于C点,CO=BO,AB=14.
x2+bx+c与x轴负半轴交于A点,与x轴正半轴交于B点,与y轴正半轴交于C点,CO=BO,AB=14.
(1)求抛物线的解析式;
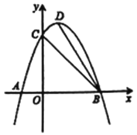
(2)如图2, 点M、N在第一象限内抛物线上,M在N点下方,连CM、CN,∠OCN+∠OCM=180°, 设M点横坐标为m,N点横坐标为n,求m与n的函数关系式(n是自变量);
(3)如图3, 在(2)条件下,连AN交CO于E,过M作MF⊥AB于F,连BM、EF,若∠AFE=2∠FMB=2β, 求N点坐标.
【答案】(1)![]() ;(2)m与n的函数关系式为
;(2)m与n的函数关系式为![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)根据题目给出条件用一个未知数舍出点A,B,C的坐标,代入解析式求解即可;
(2)根据题目给出特殊条件∠OCN+∠OCM=180°,得出直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称,设点代入即可;
对称,设点代入即可;
(3)根据二倍角关系,在大角中构造相似三角形,大胆利用一个未知数求出线段长度,利用三角形的角平分线性质求解.
解:(1)设![]() ,则
,则![]() ;
;
将![]()
![]() 代入y= -
代入y= -![]() x2+bx+c得,
x2+bx+c得,
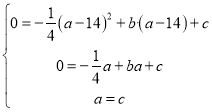 ;
;
解得: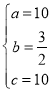 ;
;
∴抛物线的解析式:![]() ;
;
(2)∵∠OCN+∠OCM=180°;
可得直线![]() 与直线
与直线![]() 关于
关于![]() 对称;
对称;
设![]() ;
;
又![]() ;
;
可得![]() ;
;
设![]() ;
;
作点N关于![]() 的对称点
的对称点![]() ;
;
则![]() ;
;
又![]() 在
在![]() 上;
上;
![]() ;
;
化简得![]() ;
;
∴m与n的函数关系式为![]() ;
;
(3)![]() ;
;
![]() ;
;
在y正半轴上取一点H使得![]() ;
;
则有![]() ;
;
即 ;
;
解得![]() ;
;
设直线AN的解析式为:![]()
由![]() 可得
可得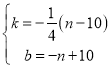 ;
;
![]() ;
;
又![]() ;
;
![]() ;
;
又![]() ;
;
![]() ;
;
在![]() 中,
中,![]() ;
;
由勾股定理可得![]() ;
;
![]() ;
;
![]() ;
;
又∵∠AFE=2∠FMB=2β;
![]() 平分
平分![]() ;
;
则有![]() ;
;
即![]() ;
;
解得![]() (舍),
(舍),![]() (舍),
(舍),![]() (舍),
(舍),![]() ;
;
![]() ;
;
![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目