题目内容
【题目】如图,一条抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 在
在![]() 轴上.
轴上.
(1)求抛物线解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,是否存在以点
,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(4)坐标平面内一点![]() 到点
到点![]() 的距离为1个单位,求
的距离为1个单位,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() 或(6,0);(3)Q(2,3)或
或(6,0);(3)Q(2,3)或![]() 或
或![]() ;(4)
;(4)![]() .
.
【解析】
解:(1)把A,B,C三点坐标代入求出解析式即可;
(2)先求出直线DB的解析式,再分①当点P在点B左侧时,②当点P在点B右侧时,分别求出P点坐标即可;
(3)分①当四边形APQC为平行四边形时,②当四边形AQPC为平行四边形时两种情况求出Q点坐标;
(4)先证△MBE∽△OBM得到![]() ,则当点D、M、E在同一直线上时,
,则当点D、M、E在同一直线上时,![]() 最短,求出最小值即可.
最短,求出最小值即可.
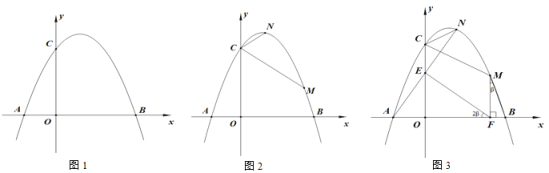
解:(1)∵抛物线与x轴交于A(-1,0),B(3,0)两点,
∴设此抛物线的解析式为y=a(x+1)(x-3),
将点C(0,3)代入,得a=-1,
∴![]() ,
,
(2)∵![]() ,
,
∴顶点D(1,4),
设直线DB解析式为y=kx+b,
将D(1,4),B(3,0)代入得,![]() ,
,
解得:k=﹣2,b=6,
∴直线DB解析式为y=﹣2x+6,
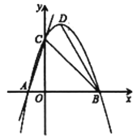
①如图1﹣1,当点P在点B左侧时,

∵∠PCB=∠CBD,
∴CP∥BD,
设直线CP解析式为y=﹣2x+m,
将C(0,3)代入,得m=3,
∴直线CP解析式y=﹣2x+3,
当y=0时,![]() ,
,
∴![]() ,
,
②如图1﹣2,当点P在点B右侧时,
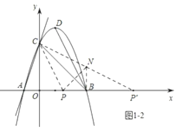
作点P关于直线BC的对称点N,延长CN交x轴于点P',此时∠P'CB=∠CBD,
∵C(0,3),B(3,0),
∴OC=OB,
∴△OBC为等腰直角三角形,
∴∠CPB=45°,
∴∠NBC=45°,
∴△PBN为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
将C(0,3),![]() 代入直线CN解析式y=nx+t,
代入直线CN解析式y=nx+t,
得: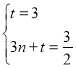 ,
,
解得,![]() ,t=3,
,t=3,
∴直线CN解析式为![]() ,
,
当y=0时,x=6,
∴P'(6,0);
综上所述,点P坐标为![]() 或(6,0);
或(6,0);
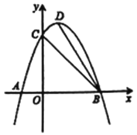
(3)①如图2﹣1,当四边形APQC为平行四边形时,

∴CQ∥AP,CQ=AP,
∵yC=3,
∴yQ=3,
令﹣x2+2x+3=3,
解得:x1=0,x2=2,
∴Q(2,3),
②如图2﹣2,当四边形AQPC为平行四边形时,
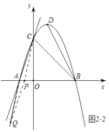
AC∥PQ,AC=PQ,
∴yC﹣yA=yP﹣yQ=3,
∵yP=0,
∴yQ=﹣3,
令﹣x2+2x+3=﹣3,
解得,![]() ,
,![]() ,
,
∴![]() ,
,![]()
综上所述,点Q的坐标为Q(2,3)或![]() 或
或![]() ;
;
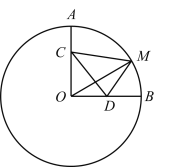
(4)∵点M到点B的距离为1个单位,
∴点M在以点B为圆心,半径为1的圆上运动,如图3
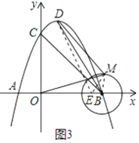
在x轴上作点![]() ,连接BM、EM、DE,
,连接BM、EM、DE,
∴![]() ,
,
∵BM=1,
∴ ,
,
∵∠MBE=∠OBM,
∴△MBE∽△OBM,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当点D、M、E在同一直线上时,![]() 最短,
最短,
∵D(1,4),
∴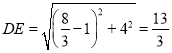 ,
,
∴![]() 的最小值为
的最小值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案