题目内容
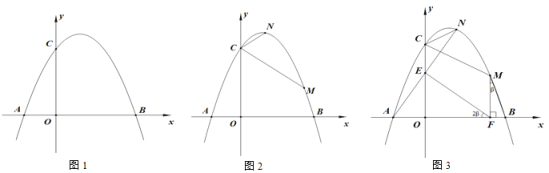
【题目】如图1,设![]() 是一个锐角三角形,且
是一个锐角三角形,且![]() ,
,![]() 为其外接圆,
为其外接圆,![]() 分别为其外心和垂心,
分别为其外心和垂心,![]() 为圆
为圆![]() 直径,
直径,![]() 为线段
为线段![]() 上一动点且满足
上一动点且满足![]() .
.
(1)证明:![]() 为
为![]() 中点;
中点;
(2)过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点,证明:
的中点,证明: ![]() ;
;
(3)直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() (如图2),以
(如图2),以![]() 为直径的圆与圆
为直径的圆与圆![]() 的另一交点为
的另一交点为![]() .证明:若
.证明:若![]() 三线共点,则
三线共点,则![]() ;反之也成立.
;反之也成立.
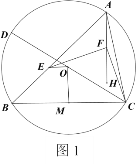

【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)连接AD,BD,得![]() ,结合H为垂心,
,结合H为垂心,![]() ,得出四边形
,得出四边形![]() 为平行四边形,得到
为平行四边形,得到![]() ,结合平行,O为CD中点,可得M为BC中点;
,结合平行,O为CD中点,可得M为BC中点;
(2)过![]() 作
作![]() ,由
,由![]() ,
, ![]() 为平行四边形,证明H为
为平行四边形,证明H为![]() 的垂心,从而得到
的垂心,从而得到![]() ;
;
(3)设![]() 与
与![]() 交点为
交点为![]() ,得到
,得到![]() ,证明H是
,证明H是![]() 的垂心,证明
的垂心,证明![]() 三线共点得
三线共点得![]() 三点共线,得到
三点共线,得到![]() .
.
解:(1)连接![]() ,则
,则![]() ,
,![]()
又![]() 为
为![]() 垂心
垂心
∴![]() ,
,![]()
∴![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]() ,又
,又![]() 为
为![]() 中点
中点
∴![]() 为
为![]() 中点
中点
(2)过![]() 作
作![]()
连接![]() ,由(1)可知四边形
,由(1)可知四边形![]() 为平行四边形,四边形
为平行四边形,四边形![]() 为平行四边形
为平行四边形
∵![]()
∴![]()
∴![]() 为
为![]() 垂心
垂心
∴![]()
∴![]()
(3)设![]() 与
与![]() 交点为
交点为![]()
由(1)可知四边形![]() 为平行四边形
为平行四边形
∴![]() 为直径
为直径![]() 中点
中点
而圆![]() 与圆
与圆![]() 相交弦为
相交弦为![]()
∴![]()
∴![]()
设![]()
则![]() 为
为![]() 垂心
垂心
∴![]()
![]() 三线共点
三线共点![]()
![]() 三点共线
三点共线
![]()
![]()
![]()
![]()

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某课外学习小组根据学习函数的经验,对函数![]() 的图象与性质进行了探究请补充完整以下探索过程:
的图象与性质进行了探究请补充完整以下探索过程:
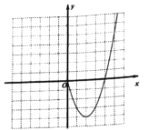
(1)列表:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出![]() ________,
________,![]() ________;
________;
(2)根据上表中的数据,在平面直角坐标系内补全该函数的图象,并结合图象写出该函数的两条性质:
性质1______________________________________________________
性质2_______________________________________________________
(3)若方程![]() 有四个不同的实数根,请根据函数图象,直接写出k的取值范围.
有四个不同的实数根,请根据函数图象,直接写出k的取值范围.