题目内容
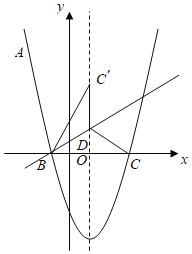
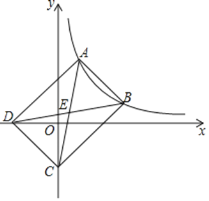
【题目】如图，点A和点B都是反比例函数
在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1，连接AB，以线段AB为边的矩形ABCD的顶点D，C恰好分别落在x轴，y轴的负半轴上，连接AC，BD交于点E，若
的面积为6，则k的值为（ ）
A.2B.3C.6D.12
【答案】B
【解析】
由点A的横坐标为1，点B的纵坐标为1，得出点E的坐标，进而推出点D的坐标，可以求出DA的长，，利用
列方程，可求出结果．
∵点A和点B都是反比例函数y＝
在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1
∴A（1，k）、B（k，1）
E为矩形ABCD对角线的交点，
∴E（
，）
∵D，C恰好分别落在x轴，y轴的负半轴上，
设D（a，0），E为点A、C的中点
∴
，
∴a=1-k，
∴D（1-k，0），
∵A（1，k）、D（1-k，0），
∴AD2=（1-k-1）2+k2=
k2，
∴AD=
∵A（1，k）、B（k，1）
∴AB=
∴
∴k2-k-6=0
解得：k=3，k=-2（不符合题意，舍去）
故选B．
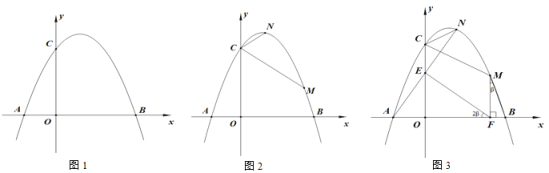
【题目】某课外学习小组根据学习函数的经验，对函数
的图象与性质进行了探究请补充完整以下探索过程：
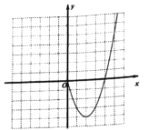
（1）列表：
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出
________，
________；
（2）根据上表中的数据，在平面直角坐标系内补全该函数的图象，并结合图象写出该函数的两条性质：
性质1______________________________________________________
性质2_______________________________________________________
（3）若方程
有四个不同的实数根，请根据函数图象，直接写出k的取值范围.
