题目内容
【题目】如图,在小正方形边长均为1的方格纸中有线段AB,点A、B均在小正方形的顶点上.

(1)以AB为一边画Rt△ABC(点C在小正方形的顶点上),使△ABC的周长为![]() +5;
+5;
(2)在(1)的条件下,以AB为一边作△ABD,(点D在小正方形的顶点上),使![]() ,且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.
,且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.
【答案】(1)图见解析;(2)图见解析;tan∠ADC=![]() .
.
【解析】
(1)由勾股定理可得AB的长为![]() ,则AC+BC的长为2
,则AC+BC的长为2![]() +5,再结合网格的特点,当AC,BC的长分别为5,2
+5,再结合网格的特点,当AC,BC的长分别为5,2![]() 时,△ABC可为直角三角形,由此画出相应的图形即可;
时,△ABC可为直角三角形,由此画出相应的图形即可;
(2)根据![]() ,且△ABD的面积为2,同时结合勾股定理以及面积法找出点D,画出相应的图形,然后再结合网格图可求出∠ADC的正切值.
,且△ABD的面积为2,同时结合勾股定理以及面积法找出点D,画出相应的图形,然后再结合网格图可求出∠ADC的正切值.
解:(1)由勾股定理可知,AB=![]() ,则AC+BC=2
,则AC+BC=2![]() +5,
+5,
如图,根据勾股定理得![]() ,
,
∴AB2+BC2=AC2,
则∠ABC=90°,△ABC的周长=5+3![]() .
.
∴如图所示的Rt△ABC即为所求;
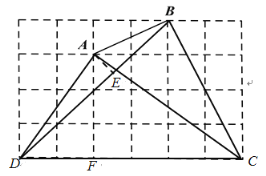
(2)如图,过点A作AE⊥BD于E,则
S△ABD=4×4-![]() ×2×3-
×2×3-![]() ×4×4-
×4×4-![]() ×1×2-1×2=2,符合题意.
×1×2-1×2=2,符合题意.
根据勾股定理可得,BD=![]() ,
,
又S△ABD=![]() ×BD×AE=
×BD×AE=![]() ×
×![]() ×AE=2,∴AE=
×AE=2,∴AE=![]() ,
,
∴BE= ,
,
此时![]() ,符合题意.
,符合题意.
∴如图所示的△ABD即可所求.
如图,在Rt△ADF中,tan∠ADF=![]() =tan∠ADC,
=tan∠ADC,
故∠ADC的正切值为![]() .
.

练习册系列答案
相关题目