题目内容
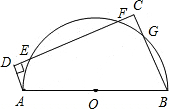
如图,ABCD是直角梯形,以斜腰AB为直径作圆,交CD于点E,F,交BC于点G.
求证:(1)DE=CF;(2)
=
.
求证:(1)DE=CF;(2)
 |
| AE |
 |
| FG |

(1)过O作OH⊥EF,H为垂足,如图,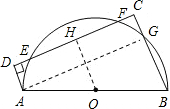
则EH=FH,OH∥AD∥BC,
而OA=OB,
∴OH为直角梯形ABCD的中位线,
∴HD=HC,
∴DE=CF;
(2)连AG,
∵AB为直径,
∴∠AGB=90°,
∴AG∥DC,
∴
=
.

则EH=FH,OH∥AD∥BC,
而OA=OB,
∴OH为直角梯形ABCD的中位线,
∴HD=HC,
∴DE=CF;
(2)连AG,
∵AB为直径,
∴∠AGB=90°,
∴AG∥DC,
∴
 |
| AE |
 |
| FG |

练习册系列答案
相关题目







