题目内容
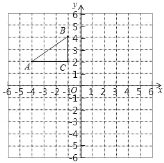
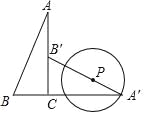
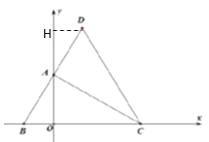
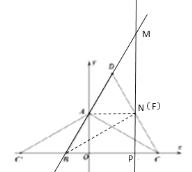
【题目】如图1,在平面直角坐标系中,![]() 的三个顶点在坐标轴上,
的三个顶点在坐标轴上,![]() ,且
,且![]() ,将
,将![]() 沿着
沿着![]() 翻折到
翻折到![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以
轴以![]() 个单位秒的速度向终点
个单位秒的速度向终点![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,分别交直线
轴,分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒,求
秒,求![]() 与
与![]() 的关系式,并写出
的关系式,并写出![]() 的取值范围.
的取值范围.
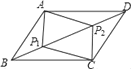
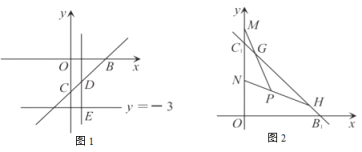
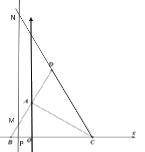
(3如图2在(2)的条件下,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 值和点
值和点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)D(![]() ,6);(2)y与x的关系式为:
,6);(2)y与x的关系式为: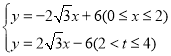 ;(3)t=3,M(2
;(3)t=3,M(2![]() ,9)
,9)
【解析】
(1)根据点坐标求出OA、OB、OC,证明△BCD是等边三角形,过点D作DH⊥y轴于H,根据折叠的性质证明△ABO≌△ADH,求出DH、AH即可得到点D的坐标;
(2)先求出直线AD与直线CD的解析式,再分直线PM在点D左侧与右侧分别求出y与x的解析式即可;
(3)根据以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形且F在直线PM上,确定点F在第一象限,根据AF=B
为顶点的四边形为平行四边形且F在直线PM上,确定点F在第一象限,根据AF=B![]() 求出t的值,即可确定点M的坐标.
求出t的值,即可确定点M的坐标.
(1)∵A(0,3),B(-![]() ,0),
,0),
∴OA=3,OB=![]() ,
,
∴AB=![]() =2
=2![]() ,
,
∵C(3![]() ,0),
,0),
∴OC=3![]() ,
,
∴AC=![]() =6,BC=4
=6,BC=4![]() ,
,
∴![]() ,
,
∴△ABC是直角三角形,且∠BAC=90°,
∴∠ABC=60°,
∴∠ACB=30°,
由折叠得:∠ACD=∠ACB=30°,∠CAD=∠BAC=90°,
∴B、A、D三点共线,∠BCD=60°,
∴△BCD是等边三角形,
过点D作DH⊥y轴于H,
由折叠得:AD=AB,
∵∠OAB=∠DAH,∠AHD=∠AOB=90°,
∴△ABO≌△ADH,
∴DH=OB=![]() ,AH=OA=3,
,AH=OA=3,
∴点D的坐标是(![]() ,6);
,6);
(2)
∵A(0,3),D(![]() ,6),∴直线AD的解析式为:y=
,6),∴直线AD的解析式为:y=![]() x+3,
x+3,
∵C(3![]() ,0),∴直线CD的解析式为:y=-
,0),∴直线CD的解析式为:y=-![]() x+9,
x+9,
当直线PM在点D的左侧时,此时![]() ,
,
MN=-![]() x+9-(
x+9-(![]() x+3)=-2
x+3)=-2![]() x+6,
x+6,
当直线PM在点D右侧时,此时![]() ,
,
MN=![]() x+3-(-
x+3-(-![]() x+9)=2
x+9)=2![]() x-6,
x-6,
综上,y与t的关系式为: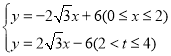 ;
;
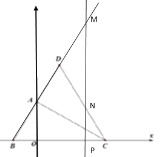
(3)∵点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,C(3
轴的对称点,C(3![]() ,0),
,0),
∴![]() (-3
(-3![]() ,0),
,0),
∴B![]() =2
=2![]() ,
,
∵以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形,且F在直线PM上,
为顶点的四边形为平行四边形,且F在直线PM上,
∴点F在第一象限,且AF=B![]() =2
=2![]() ,AF∥B
,AF∥B![]() ,
,
令直线CD的解析式y=-![]() x+9中y=3时,得x=2
x+9中y=3时,得x=2![]() ,
,
∴N(2![]() ,3),
,3),
∴AN∥x轴,
∴点F与点N重合,
∴点M的横坐标为2![]() ,
,
将x=2![]() 代入y=
代入y=![]() x+3中得y=9,
x+3中得y=9,
∴点M的坐标为(2![]() ,9),
,9),
∵点P的横坐标是2![]() ,
,
∴t=![]() .
.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案