题目内容
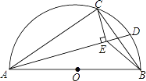
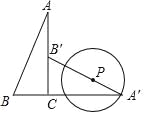
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,AB=13,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为_____.
,AB=13,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B′上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为_____.
【答案】![]()
【解析】
先根据直角三角形的性质和勾股定理,结合sinA=513,AC=12求出AB与BC的长,再对⊙P与△ABC相切的位置进行讨论;
①如图1中,当⊙P与直线AC相切于点Q时,连接PQ,根据题意可得PQ∥CA′,从而得到PQCA'=PB'A'B',代入已知条件求出PQ,即为圆的半径;
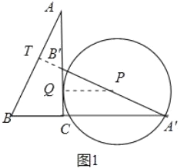
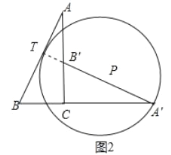
②如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,从而得到△A′BT∽△ABC.利用相似三角形对应边成比例得到A'TAC=A'BAB,求出A′T确定圆的直径,进而求出半径.
∵在△ABC中,∠ACB=90°,sinA=513,AC=12,
∴BC=5,AB=13.
①当⊙P与直线AC相切于点Q时,连接PQ,如图1所示:
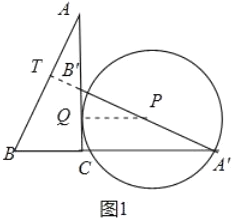
设PQ=PA′=r.
∵PQ∥CA′,
∴PQ:CA'=PB':A'B',
∴r:12=(13r):13,
∴r=![]() .
.
②当⊙P与AB相切于点T时,如图2所示,易证A′、B′、T共线.
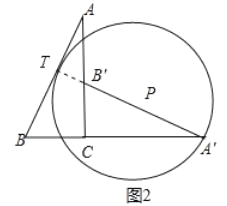
∵△A′BT∽△ABC,
∴A'T:AC=A'B:AB,
∴A'T:12=17:13,
∴A′T=![]() ,
,
∴r=![]() A′T=
A′T=![]() .
.
综上所述,⊙P的半径为![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目