题目内容
【题目】已知点![]() ,直线
,直线![]() 无论
无论![]() 取何值,直线总过定点
取何值,直线总过定点![]() .
.
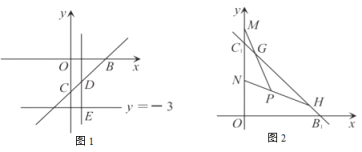
(1)求定点![]() 的坐标;
的坐标;
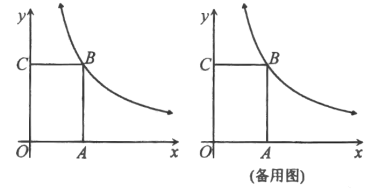
(2)如图1,若点![]() 为直线
为直线![]() 上(点
上(点![]() 除外)一动点,过点
除外)一动点,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,距离
上,距离![]() 点为
点为![]() 个单位,
个单位,![]() 点横坐标为
点横坐标为![]() 的面积为
的面积为![]() ,求
,求![]() 与的函数关系式;
与的函数关系式;
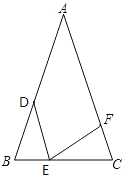
(3)若直线![]() 关于
关于![]() 轴对称后再向上平移
轴对称后再向上平移![]() 个单位得到直线
个单位得到直线![]() ,如图2, 点
,如图2, 点![]() 和
和![]() 是直线
是直线![]() 上两点,点
上两点,点![]() 为第一象限内(
为第一象限内(![]() 两点除外)的一点,且
两点除外)的一点,且![]() ,直线
,直线![]() 和
和![]() 分别交
分别交![]() 轴于点
轴于点![]() 两点,问线段
两点,问线段![]() 有什么数量关系,并给出证明.
有什么数量关系,并给出证明.
【答案】(1)定点![]() ;(2)
;(2)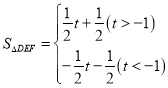 ;(3)
;(3)![]() .证明见解析.
.证明见解析.
【解析】
(1)由y=k(x-2),可得x=2时,y=0,可知定点B(2,0);
(2)求出DE的长,分两种情形分别求解即可解决问题;
(3)求出直线PG、PH的解析式,得到点M、N的坐标即可解决问题;
解:![]() 与
与![]() 无关,
无关,
![]() ,
,
![]() ,
,
∴定点为![]() ;
;
![]() 把(0,-2)代入y=kx-2k,得到k=1,
把(0,-2)代入y=kx-2k,得到k=1,
∴直线BC的解析式为:y=x-2,
∵OB=OC=2,
∴∠OBC=45°,
![]() ,
,
又![]() ,
,
![]() ,
,
过点F作FH⊥DE,连接EF,如图:
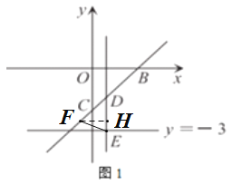
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
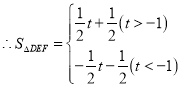 ;
;
![]() ,
,
证明:根据题意可知,直线![]() ,
,
![]() 点
点![]() 和
和![]() ,点在
,点在![]() 上,
上,
![]() ,
,
又![]() ,
,
![]() ,
,
由![]() 和
和![]() 得直线
得直线![]() 的解析式:
的解析式:![]() ,
,
![]() ,
,
由![]() 和
和![]() 得直线
得直线![]() 的解析式:
的解析式:![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目