��Ŀ����
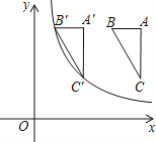
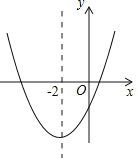
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ����������Ϊ����2����9a�������н��ۣ���4a+2b+c��0����5a��b+c=0����������a��x+5����x��1��=��1��������x1��x2����x1��x2����5��x1��x2��1����������|ax2+bx+c|=1���ĸ����������ĸ����ĺ�Ϊ��4��������ȷ�Ľ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�B
�����������������ߵĶ������꣨��2����9a�������ݶ������깫ʽ�����b=4a��c=-5a���Ӷ��ɵ������ߵĽ���ʽΪy=ax2+4ax��5a��Ȼ����ݶ��κ���������һһ�жϼ��ɣ�
��a>0��
�������ߵĶ������꣨��2����9a����
����![]() =��2��
=��2��![]() =��9a��
=��9a��
��b=4a��c=-5a��
�������ߵĽ���ʽΪy=ax2+4ax��5a��
��4a+2b+c=4a+8a��5a=7a��0���ʢ���ȷ��
5a��b+c=5a��4a��5a=��4a��0���ʢڴ���
��������y=ax2+4ax��5a��x���ڣ���5��0������1��0����
��������a��x+5����x��1��=��1��������x1��x2����x1��x2����5��x1��x2��1����ȷ���ʢ���ȷ��
������|ax2+bx+c|=1���ĸ����������ĸ����ĺ�Ϊ��8���ʢܴ���
��ѡB��

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
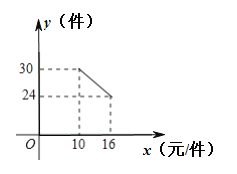
������������Ӧ����ϵ�д�����Ŀ��ij������ʦ����˶��ֻ����п��߶��������ζ�����������������һ�ζ�����ȣ�����ʦ�ڶ��ζ������������İٷ�������ƽ���������ٵİٷ��ʵ�3����������ʦ�ڶ��ζ���ʱƽ���������ٵİٷ���Ϊ![]() ��
��
��Ŀ | ��һ�ζ��� | �ڶ��ζ��� |
����(��) | 10000 | ____________ |
ƽ������(��/��) | 0.6 | ____________ |
����(��) | 6000 | 7020 |
ע��������ƽ�����������룮
(1)����������ɱ�����գ�
(2)��x��
(3)����ʦ���ֺ����в���������һΪ24000������������ζ���������������500�ף�ʹ���ܲ���ǡ��Ϊ24000����������ʦ��500��ƽ��������
����Ŀ������������Ʊ�۸����±���ʾ��
��Ʊ���� | 1��50�� | 51��100�� | 100������ |
ÿ����Ʊ�� | 13Ԫ | 11Ԫ | 9Ԫ |
ijУ��һ��1����2��������ȥ���������������У�1�����������٣�����50�ˣ���2���������϶࣬��50���ˣ������������������100��. ����������Ϊ��λ�ֱ�Ʊ����һ��Ӧ��1240Ԫ�����������������������Ϊһ�����幺Ʊ����ֻ�踶936Ԫ.
��1���з��̻��������������ж���ѧ����
��2����������������Ʊ���Dz��dz�һ��1�����ѧ����Ҫ��13Ԫ��Ʊ�أ�����ʲôʡǮ��ʽ����������Ʊ�أ�˵˵�������.
��3������Ϊ�Ƿ���������Ŀ��ܣ�51��100��֮����Ʊ��Ǯ����100��������Ʊ��Ǯ����ȣ�����У��Ƕ��������������ƱǮ����ȣ�