Question

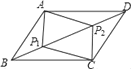
【题目】如图，在ABCD中，P1、P2是对角线BD的三等分点．求证：四边形APlCP2是平行四边形．

Answer 1

【答案】见解析

【解析】

由题意可得 BP1=DP2， AB=CD，AB//CD，根据平行线的性质可得∠ABP1=∠CDP2，证明△ABP1≌△CDP2，根据全等三角形的性质可得AP1=CP2，同理可证：CP1=AP2，根据两组对边分别相等的四边形是平行四边形即可得结论.

∵P1，P2是对角线BD的三等分点，ABCD是平行四边形，

∴BP1=DP2， AB=CD，AB//CD，

∴∠ABP1=∠CDP2，

在△ABP1和△CDP2中，

，

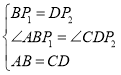∴△ABP1≌△CDP2(SAS)，

∴AP1=CP2，

同理可证：CP1=AP2，

∴四边形AP1CP2是平行四边形.