题目内容
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
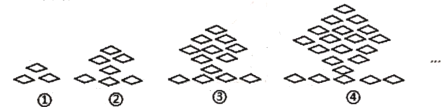
(1)填写下表:
图形序号 | 菱形个数(个) |
① | 3 |
② | 7 |
③ | ________ |
④ | ________ |
…… | …… |
(2)根据表中规律猜想,图n中菱形的个数_______(用含n的式子表示);
(3)是否存在一个图形恰好由111个菱形组成?若存在,求出图的序号;若不存在,说明理由.
【答案】(1)③ 13,④ 21;(2)图n中菱形的个数![]() (3)存在,是图⑩.
(3)存在,是图⑩.
【解析】
(1)观察图形,数出图③、图④中菱形的个数;
(2)设图n中菱形的个数为an(n为正整数),观察图形,找出部分图形中菱形的个数,根据菱形个数的变化(分成上下两部分,根据两部分的变化)可找出变化规律“an=n2+n+1(n为正整数)”;
(3)由(2)的结论结合菱形的个数为111,即可得出关于n的一元二次方程,解之取其正值(正整数值)即可得出结论.
(1)观察图形,可知:图③中有13个菱形,图④中有21个菱形.
故答案为:13;21.
(2)设图n中菱形的个数为an(n为正整数),
观察图形,可知:a1=3=1+2,a2=7=4+3,a3=13=9+4,a4=21=16+5,…,
∴an=n2+n+1(n为正整数).
(3)依题意,得:n2+n+1=111,
解得:n1=-11(舍去),a2=10,
∴存在一个图形恰好由111个菱形组成,该图形的序号为⑩.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 270 | 500元 |
餐椅 | a﹣110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)求表中a的值;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
(3)由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,但销售价格保持不变.商场购进了餐桌和餐椅共200张,应怎样安排成套销售的销售量(至少10套以上),使得实际全部售出后,最大利润与(2)中相同?请求出进货方案和销售方案.