题目内容
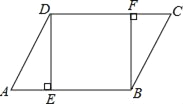
【题目】如图,在ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE为矩形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由DE与AB垂直,BF与CD垂直,得到一对直角相等,再由ABCD为平行四边形得到AD=BC,对角相等,利用AAS即可的值;
(2)由平行四边形的对边平行得到DC与AB平行,得到∠CDE为直角,利用三个角为直角的四边形为矩形即可的值.
试题解析:(1)∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°,
∵四边形ABCD为平行四边形,
∴AD=BC,∠A=∠C,
在△ADE和△CBF中,
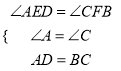 ,
,
∴△ADE≌△CBF(AAS);
(2)∵四边形ABCD为平行四边形,
∴CD∥AB,
∴∠CDE+∠DEB=180°,
∵∠DEB=90°,
∴∠CDE=90°,
∴∠CDE=∠DEB=∠BFD=90°,
则四边形BFDE为矩形.

练习册系列答案
相关题目
【题目】已知某山区的平均气温与该山的海拔高度的关系见下表:
海拔高度(单位:米) | 0 | 100 | 200 | 300 | 400 | … |
平均气温(单位:℃) | 22 | 21.5 | 21 | 20.5 | 20 | … |
(1)若海拔高度用x(米)表示,平均气温用y(℃)表示,试写出y与x之间的函数关系式;
(2)若某种植物适宜生长在18℃~20℃(包含18℃,也包含20℃)山区,请问该植物适宜种植在海拔为多少米的山区?