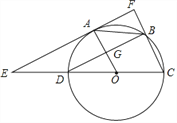
题目内容
【题目】我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.
概念理解:在“矩形、菱形和正方形”这三种特殊四边形中,不一定是“等邻角四边形”的是______.
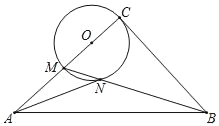
问题探究:如图,在等邻角四边形ABCD中,∠B=∠C,AB=3,BC=9,P为线段BC上一动点(不包含端点B,C),Q为直线CD上一动点,连结PA,PQ,在P,Q的运动过程中始终满足∠APQ=∠B,当CQ达到最大时,试求此时BP的长.
应用拓展:在以60°为等角的等邻角四边形ABCD中,∠D=90°,若AB=3,AD=![]() ,试求等邻角四边形ABCD的周长.
,试求等邻角四边形ABCD的周长.
【答案】概念理解:菱形;问题探究:当CQ达到最大时,此时BP的长是![]() ;应用拓展:等邻角四边形ABCD的周长为12+
;应用拓展:等邻角四边形ABCD的周长为12+![]() 或6
或6![]() -3.
-3.
【解析】
概念理解:根据等邻边四边形的定义即可解答;问题探究:设BP=x,CQ=y,则PC=9-x,根据两角对应相等两三角形相似证明△PBA∽△QCP,列比例式可得:![]() ,则y=-
,则y=-![]() +3x=-
+3x=-![]() (x-
(x-![]() )2+
)2+![]() ,根据二次函数的最值可得结论;应用拓展:准确画图后作辅助线,构建直角三角形,根据直角三角形30°角的性质和勾股定理可求得四边形各边的长,相加可得周长.
,根据二次函数的最值可得结论;应用拓展:准确画图后作辅助线,构建直角三角形,根据直角三角形30°角的性质和勾股定理可求得四边形各边的长,相加可得周长.
概念理解:
①∵矩形的四个角都是直角,
根据“等邻角四边形”的定义,
得到矩形是“等邻角四边形”;
②同理可得:正方形是“等邻角四边形”,
③∵菱形的对角相等,邻角互补,但不一定相等,
∴菱形不一定是“等邻角四边形”;
故答案为:菱形;
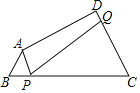
问题探究:
如图,设BP=x,CQ=y,则PC=9-x,
∵∠APB+∠APQ+∠CPQ=180°,
∴∠APB+∠CPQ=180°-∠APQ,
∵∠CPQ+∠C+∠CQP=180°,
∴∠CPQ+∠CQP=180°-∠C,
∵∠C=∠APQ,
∴∠APB+∠CPQ=∠CPQ+∠CQP,
∴∠APB=∠CQP,
∵∠B=∠C,
∴△PBA∽△QCP,
∴![]() ,
,
∴![]() ,
,
∴y=-![]() +3x=-
+3x=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∵-![]() <0,
<0,
∴当x=![]() 时,y有最大值是
时,y有最大值是![]() ,
,
即当CQ达到最大时,此时BP的长是![]() ;.
;.
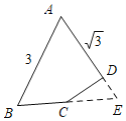
应用拓展:
(3)有两种情况:
①当∠B=∠C=60°时,
如图,延长DA,CB交于E,过B作BF⊥DE于F,
∵∠C=60°,
∴∠E=30°,
∵∠ABC=60°,
∴∠BAE=∠E=30°,
∴AB=BE=3,
∴BF=![]() ,EF=AF=
,EF=AF=![]() ,
,
∴DE=AD+AE=![]() +3
+3![]() =4
=4![]() ,
,
Rt△DCE中,设CD=x,则CE=2x,
由勾股定理得:x2+(4![]() )2=(2x)2,
)2=(2x)2,
x=±4,
∴CE=8,CD=4,
∴BC=8-3=5,
∴四边形ABCD的周长=AB+BC+CD+AD=3+5+4+![]() =12+
=12+![]() .
.
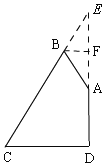
②当∠A=∠B=60°时,如图所示:
延长AD、BC交于点E,
∵∠A=∠B=60°,
∴△ABE是等边三角形,
∴∠E=60°,
∵∠ADC=90°,
∴∠DCE=30°,
∵AB=3,AD=![]() ,
,
∴DE=3-![]() ,CE=6-2
,CE=6-2![]() ,CD=
,CD=![]() DE=3
DE=3![]() -3,
-3,
∴BC=3-(6-2![]() )=2
)=2![]() -3,
-3,
∴四边形ABCD的周长=AB+BC+CD+AD=3+2![]() -3+3
-3+3![]() -3+
-3+![]() =6
=6![]() -3;
-3;
综上,等邻角四边形ABCD的周长为12+![]() 或6
或6![]() -3.
-3.

【题目】某班准备选一名学生参加数学史知识竞赛,现统计了两名选手本学期的五次测试 成绩:甲:83,80,90,87, 85; 乙:78,92,82,89,84.
(1)请根据上面的数据完成下表:
极差 | 平均数 | 方差 | |
甲 | 10 | ________ | ________ |
乙 | _________ | 85 | 24.8 |
(2)请你推选出一名参赛选手,并用所学的统计知识说明理由.