题目内容
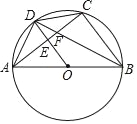
【题目】如图,四边形ABCD内接于⊙O,BC=CD,∠C=2∠BAD.
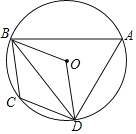
(1)求∠BOD的度数;
(2)求证:四边形OBCD是菱形;
(3)若⊙O的半径为r,∠ODA=45°,求△ABD的面积(用含r的代数式表示).
【答案】(1)120°;(2)证明见解析;(3)(1+![]() )r2.
)r2.
【解析】
(1)结合圆的内接四边形对角互补,运用方程思想,再运用圆周角定理求解即可;
(2)连接OC,证明△BOC和△DOC都是等边三角形,进而即可证明结论;
(3)分别计算△BOD,△AOD和△AOB的面积,再求和即可.
(1)∵四边形ABCD内接于⊙O,
∴∠C+∠BAD=180°,
∵∠C=2∠BAD,
∴∠C=120°,∠BAD=60°,
∴∠BOD=2∠BAD=120°;
(2)如图1连接OC,
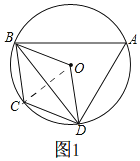
∵BC=CD,
∴∠BOC=∠DOC=60°,
∵OB=OC=OD,
∴△BOC和△DOC都是等边三角形,
∴OB=OC=OD=BC=DC,
∴四边形OBCD是菱形,
(3)如图2,连接OA,过点A作BO的垂线交BO的延长线于点N,
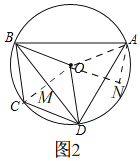
∵∠BOD=120°,OB=OD,
∴∠ODM=30°,
∵∠BOM=∠DOM,
∴OM⊥BD,
∴OM=![]() r,DM=
r,DM=![]() r,
r,
∴BD=2DM=![]() r,
r,
∴S△BOD=![]() r2,
r2,
∵∠ODA=45°,OA=OD,
∴∠OAD=∠ODA=45°,
∴∠AOD=90°,
∴S△AOD=![]() r2,
r2,
∵∠BOD=120°,∠AOD=90°,
∴∠AOB=150°,
∴∠AON=30°,
∴AN=![]() OA=
OA=![]() r,
r,
∴S△AOB=![]() r2,
r2,
∴△ABD的面积为![]() r2+
r2+![]() r2+
r2+![]() r2=(1+
r2=(1+![]() )r2.
)r2.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目