题目内容
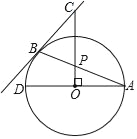
【题目】如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD⊥CE 于点 D,AC 平分∠DAB.
(1) 求证:直线 CE 是⊙O 的切线;
(2) 若 AB=10,CD=4,求 BC 的长.

【答案】(1)证明见解析;(2)BC=2![]() 或4
或4![]() .
.
【解析】
(1)如图,连接OC,由AC平分∠DAB得到∠DAC=∠CAB,然后利用等腰三角形的性质得到∠OCA=∠CAB,接着利用平行线的判定得到AD∥CO,而CD⊥AD,由此得到CD⊥AD,最后利用切线的判定定理即可证明CD为⊙O的切线;
(2)证明△DAC∽△CAB,根据相似三角形对应边成比例进行求解即可.
(1)如图,连接OC
∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠OCA=∠CAB,
∴∠OCA=∠DAC,
∴AD∥CO,
∵CD⊥AD,
∴OC⊥CD,
∵OC是⊙O直径且C在半径外端,
∴CD为⊙O的切线;
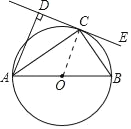
(2)∵AB是直径,
∴∠ACB=90°,
∵AD⊥CD,
∴∠ADC=∠ACB=90°,
∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴![]() ,
,
∴BCAC=DCAB=4×10=40,
∵BC2+AC2=100,
∴(BC+AC)2=BC2+AC2+2BCAC=180,(BC-AC)2= BC2+AC2-2BCAC=20,
∴BC+AC=6![]() ,AC﹣BC=2
,AC﹣BC=2![]() 或BC﹣AC=2
或BC﹣AC=2![]() ,
,
∴BC=2![]() 或4
或4![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目