ƒøƒ⁄»ð
°æƒø°ø“—÷™≈◊ŒÔœþy£Ωax2+bx+c£®a°Ÿ0£©”Îx÷·Ωª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨µ„B∫Õµ„Cµƒ◊¯±Í∑÷±Œ™£®3£¨0£©°¢£®0£¨©Å3£©£¨≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™x£Ω1£¨DŒ™≈◊ŒÔœþµƒ∂•µ„£Æ
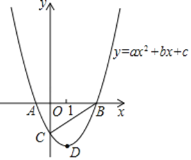
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£Æ
£®2£©µ„EŒ™œþ∂ŒBC…œ“ª∂ص„£¨π˝µ„E◊˜x÷·µƒ¥πœþ£¨”Î≈◊ŒÔœþΩª”⁄µ„F£¨«ÛÀƒ±þ–ŒACFB√ʪ˝µƒ◊Ó¥Û÷µ£¨“‘º∞¥À ±µ„Eµƒ◊¯±Í£Æ
£®3£©≈◊ŒÔœþµƒ∂‘≥∆÷·…œ «∑ҥʑ⁄“ªµ„P£¨ π°˜PCDŒ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨–¥≥ˆµ„Pµ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©y£Ωx2©Å2x©Å3£ª£®2£©Àƒ±þ–ŒACFB√ʪ˝µƒ◊Ó¥Û÷µŒ™![]() £¨¥À ±µ„Eµƒ◊¯±ÍŒ™£®
£¨¥À ±µ„Eµƒ◊¯±ÍŒ™£®![]() £¨©Å
£¨©Å![]() £©£ª£®3£©¥Ê‘⁄¬˙◊„Ãıº˛µƒPµ„£¨∆‰◊¯±ÍŒ™£®1£¨©Å3£©ªÚ£®1£¨©Å2£©ªÚ£®1£¨©Å4+
£©£ª£®3£©¥Ê‘⁄¬˙◊„Ãıº˛µƒPµ„£¨∆‰◊¯±ÍŒ™£®1£¨©Å3£©ªÚ£®1£¨©Å2£©ªÚ£®1£¨©Å4+![]() £©ªÚ£®1£¨©Å4©Å
£©ªÚ£®1£¨©Å4©Å![]() £©
£©
°æΩ‚Œˆ°ø
£®1£©”…B°¢Cµƒ◊¯±Í£¨Ω·∫œ≈◊ŒÔœþ∂‘≥∆÷·£¨∏˘æð¥˝∂®œµ ˝∑®ø…«Ûµ√≈◊ŒÔœþΩ‚Œˆ Ω£ª
£®2£©”…B°¢C◊¯±Íø…«Ûµ√÷±œþBCΩ‚Œˆ Ω£¨…Ë≥ˆFµ„◊¯±Í£¨‘Úø…±Ì æ≥ˆEµ„◊¯±Í£¨¥”∂¯ø…«Ûµ√EFµƒ≥§£¨‘Úø…±Ì æ≥ˆ°˜CBFµƒ√ʪ˝£¨¥”∂¯ø…±Ì æ≥ˆÀƒ±þ–ŒACFBµƒ√ʪ˝£¨‘Ÿ¿˚”√∂˛¥Œ∫Ø ˝µƒ–‘÷ ø…«Û∆‰◊Ó¥Û÷µ£¨Ω¯∂¯«Û≥ˆEµ„µƒ◊¯±Í£ª
£®3£©”…≈◊ŒÔœþΩ‚Œˆ Ωø…«Ûµ√Dµ„◊¯±Í£¨ø……ËPµ„◊¯±ÍŒ™£®1£¨t£©£¨‘Úø…±Ì æ≥ˆPC°¢PD∫ÕCDµƒ≥§£¨”…µ»—¸»˝Ω«–Œø…∑÷PC£ΩPD°¢PC£ΩCD∫ÕPD£ΩCD»˝÷÷«Èøˆ£¨∑÷±µ√µΩπÿ”⁄tµƒ∑Ω≥㨺¥ø…«Ûµ√Pµ„◊¯±Í£Æ
Ω‚£∫£®1£©°þµ„B∫Õµ„Cµƒ◊¯±Í∑÷±Œ™£®3£¨0£©£®0£¨©Å3£©£¨≈◊ŒÔœþµƒ∂‘≥∆÷·Œ™x£Ω1£¨
°ý £¨Ω‚µ√
£¨Ω‚µ√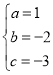 £¨
£¨
°ý≈◊ŒÔœþΩ‚Œˆ ΩŒ™y£Ωx2©Å2x©Å3£ª
£®2£©£©…Ë÷±œþBCΩ‚Œˆ ΩŒ™y£Ωkx+b£¨
¥˙»ÎB£®3£¨0£©£¨C£®0£¨©Å3£©µ√![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
°ý÷±œþBCΩ‚Œˆ ΩŒ™y£Ωx©Å3£¨

°þEµ„‘⁄÷±œþBC…œ£¨Fµ„‘⁄≈◊ŒÔœþ…œ£¨
°ý…ËF£®x£¨x2©Å2x©Å3£©£¨E£®x£¨x©Å3£©£¨
°þµ„F‘⁄œþ∂ŒBCœ¬∑Ω£¨
°ýEF£Ωx©Å3©Å£®x2©Å2x©Å3£©£Ω©Åx2+3x£¨
°ýS°˜BCF£Ω![]() EFOB£Ω
EFOB£Ω![]() °¡3£®©Åx2+3x£©£Ω©Å
°¡3£®©Åx2+3x£©£Ω©Å![]() x2+
x2+![]() x£Ω©Å
x£Ω©Å![]() £®x©Å
£®x©Å![]() £©2+
£©2+![]() £¨
£¨
”÷°þS°˜ABC£Ω![]() ABOC£Ω
ABOC£Ω![]() °¡4°¡3£Ω6£¨
°¡4°¡3£Ω6£¨
°ýSÀƒ±þ–ŒACFB£ΩS°˜ABC+S°˜BCF£Ω6©Å![]() £®x©Å
£®x©Å![]() £©2+
£©2+![]() £Ω©Å
£Ω©Å![]() £®x©Å
£®x©Å![]() £©2+
£©2+![]() £¨
£¨
°þ©Å![]() £º0£¨
£º0£¨
°ýµ±x£Ω![]() ±£¨SÀƒ±þ–ŒACFB”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™
±£¨SÀƒ±þ–ŒACFB”–◊Ó¥Û÷µ£¨◊Ó¥Û÷µŒ™![]() £¨¥À ±Eµ„◊¯±ÍŒ™£®
£¨¥À ±Eµ„◊¯±ÍŒ™£®![]() £¨©Å
£¨©Å![]() £©£¨
£©£¨
◊€…œø…µ√£∫Àƒ±þ–ŒACFB√ʪ˝µƒ◊Ó¥Û÷µŒ™![]() £¨¥À ±µ„Eµƒ◊¯±ÍŒ™£®
£¨¥À ±µ„Eµƒ◊¯±ÍŒ™£®![]() £¨©Å
£¨©Å![]() £©£ª
£©£ª
£®3£©°þy£Ωx2©Å2x©Å3£Ω£®x©Å1£©2©Å4£¨
°ýD£®1£¨©Å4£©£¨«“C£®0£¨©Å3£©£¨
°þPµ„Œ™≈◊ŒÔœþ∂‘≥∆÷·…œµƒ“ªµ„£¨
°ý…ËP£®1£¨t£©£¨
°ýPC£Ω![]() £Ω
£Ω![]() £¨PD£Ω|t+4|£¨CD£Ω
£¨PD£Ω|t+4|£¨CD£Ω![]() £Ω
£Ω![]() £¨
£¨
°þ°˜PCDŒ™µ»—¸»˝Ω«–Œ£¨
°ý∑÷PC£ΩPD°¢PC£ΩCD∫ÕPD£ΩCD»˝÷÷«Èøˆ£¨
¢Ÿµ±PC£ΩPD ±£¨‘Ú![]() £Ω|t+4|£¨Ω‚µ√t£Ω©Å3£¨
£Ω|t+4|£¨Ω‚µ√t£Ω©Å3£¨
°ý¥À ±Pµ„◊¯±ÍŒ™£®1£¨©Å3£©£ª
¢⁄µ±PC£ΩCD ±£¨‘Ú![]() £Ω
£Ω![]() £¨Ω‚µ√t£Ω©Å2ªÚt£Ω©Å4£®”ÎDµ„÷ÿ∫œ£¨…·»•£©£¨
£¨Ω‚µ√t£Ω©Å2ªÚt£Ω©Å4£®”ÎDµ„÷ÿ∫œ£¨…·»•£©£¨
°ý¥À ±Pµ„◊¯±ÍŒ™£®1£¨©Å2£©£ª
¢€µ±PD£ΩCD ±£¨‘Ú|t+4|£Ω![]() £¨Ω‚µ√t£Ω©Å4+
£¨Ω‚µ√t£Ω©Å4+![]() ªÚt£Ω©Å4©Å
ªÚt£Ω©Å4©Å![]() £¨
£¨
°ý¥À ±Pµ„◊¯±ÍŒ™£®1£¨©Å4+![]() £©ªÚ£®1£¨©Å4©Å
£©ªÚ£®1£¨©Å4©Å![]() £©£ª
£©£ª
◊€…œø…÷™£¨¥Ê‘⁄¬˙◊„Ãıº˛µƒPµ„£¨∆‰◊¯±ÍŒ™£®1£¨©Å3£©ªÚ£®1£¨©Å2£©ªÚ£®1£¨©Å4+![]() £©ªÚ£®1£¨©Å4©Å
£©ªÚ£®1£¨©Å4©Å![]() £©£Æ
£©£Æ

°æƒø°ø‘⁄“ª∏ˆ≤ªÕ∏√˜µƒ¥¸◊”÷–◊∞”–≥˝—’…´Õ‚∆‰”ýæ˘œýÕ¨µƒm∏ˆ–°«Ú£¨∆‰÷– 5 ∏ˆ∫⁄«Ú£¨ ¥”¥¸÷–Àʪ˙√˛≥ˆ“ª«Ú£¨º«œ¬∆‰—’…´£¨’‚≥∆Œ™“¿¥Œ√˛«Ú ‘—È£¨÷Æ∫Û∞—À¸∑≈ªÿ¥¸ ÷–£¨Ω¡‘»∫Û£¨‘ŸºÃ–¯√˛≥ˆ“ª«Ú£Æ“‘œ¬ «¿˚”√º∆À„ª˙ƒ£ƒ‚µƒ√˛«Ú ‘—È¥Œ ˝”Î√˛≥ˆ∫⁄«Ú¥Œ ˝µƒ¡–±Ì£∫
√˛«Ú ‘—È¥Œ ˝ | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
√˛≥ˆ∫⁄«Ú¥Œ ˝ | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
∏˘æ𡖱̣¨ø…“‘π¿º∆≥ˆ m µƒ÷µ «£® £©
A. 5 B. 10 C. 15 D. 20