题目内容
【题目】已知:如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 为⊙
为⊙![]() 外一点,
外一点,![]() ,垂足为
,垂足为![]() ,弦
,弦![]() ,且
,且![]() ,
,![]() .
.
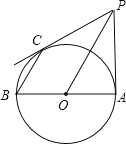
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)求⊙![]() 的半径.
的半径.
【答案】(1)见解析;(2)⊙![]() 的半径为
的半径为![]() .
.
【解析】
(1)连接OC,要证明PC是⊙O的切线只要证明∠OCP=90°即可,利用已知条件可以证明△PCO≌△PAO,即可得到∠OCP=∠OAP=90°;
(2)在Rt△AOP中根据含30°角的直角三角形的性质解答即可.
(1)证明:如图,连接OC,
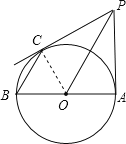
∵BC∥OP,
∴∠B=∠POA,∠BCO=∠COP,
∵OB=OC,
∴∠B=∠OCB,
∴∠COP=∠AOP;
∵OC=OA,OP=OP,
∴△PCO≌△PAO(SAS),
∴∠OCP=∠OAP=90°,
∴PC是⊙O的切线;
(2)解:∵∠APC=60°,
由(1)可得△PCO≌△PAO,∴∠OPA=∠OPC,
∴∠OPA=30°,
∵∠PAO=90°,AP=2![]() ,
,
∴OP=2OA,
根据勾股定理可得OA=2,
即⊙O的半径为2.

练习册系列答案
相关题目