题目内容
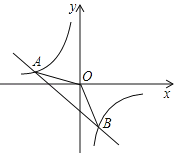
【题目】如图，一次函数
的图象与反比例函数
的图象相交于A（2，1），B两点．
（1）求出反比例函数与一次函数的表达式；
（2）请直接写出B点的坐标，并指出使反比例函数值大于一次函数值的x的取值范围．
【答案】（1）
，
；（2）B（﹣1，﹣2），x＜﹣1或0＜x＜2．
【解析】
（1）先将点A（2，1）代入
求得k的值，再将点A（2，1）代入
，求得m即可．
（2）当反比例函数的值大于一次例函数的值时，即一次函数的图象在反比例函数的图象下方时，x的取值范围．
解：（1）将A（2，1）代入中，得k=2×1=2，
∴反比例函数的表达式为，将A（2，1）代入中，得2+m=1，
∴m=﹣1，
∴一次函数的表达式为
；
（2）解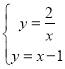
得
或
所以B（﹣1，﹣2）；
当x＜﹣1或0＜x＜2时，反比例函数的值大于一次函数的值．
练习册系列答案
相关题目
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋中并搅匀，让学生进行摸球试验，每次摸出一个球（放回），下表是活动进行中的一组统计数据．
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | _____ | _____ | _____ |
（1）补全上表中的有关数据，根据上表数据估计从袋中摸出一个黑球的概率是______．（结果都保留小数点后两位）
（2）估算袋中白球的个数为________．
（3）在（2）的条件下，若小强同学有放回地连续两次摸球，用画树状图或列表的方法计算出两次都摸出白球的概率．