题目内容
【题目】如图，
中，
，
于
，
，
为
边上一点．
（1）当
时，直接写出
，
．
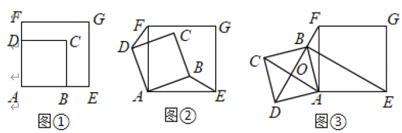
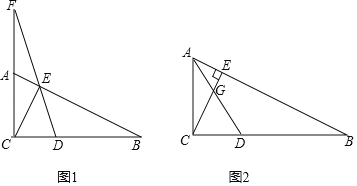
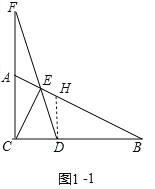
（2）如图1，当，
时，连
并延长交
延长线于
，求证：
．
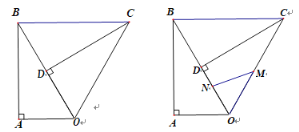
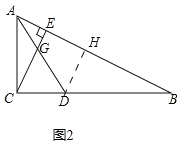
（3）如图2，连
交
于
，当
且
时，求
的值．
【答案】（1）
，
；（2）证明见解析；（3）
．
【解析】
（1）利用相似三角形的判定可得
，列出比例式即可求出结论；
（2）作
交
于
，设
，则
，根据平行线分线段成比例定理列出比例式即可求出AH和EH，然后根据平行线分线段成比例定理列出比例式即可得出结论；
（3）作
于，根据相似三角形的判定可得
，列出比例式可得
，设
，
，
，即可求出x的值，根据平行线分线段成比例定理求出
，设
，
，
，然后根据勾股定理求出AC，即可得出结论．
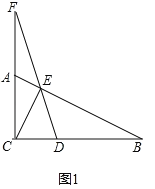
（1）如图1中，当
时，
．
，
，
，
，
，
，
．
故答案为：，．
（2）如图
中，作交于．
，
，
∴tan∠B=
，tan∠ACE= tan∠B=
∴BE=2CE，
，
，设，则，
，
，
，
，
，
，
．
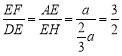（3）如图2中，作于．
，
，
，
，
，
，
，
，
，
，
，设，，，
则有
，
解得
或
(舍弃)，
，
，
，
，
，，
，
，
，
，设，，，
在
中，
，
，
，
，
．
练习册系列答案
相关题目
