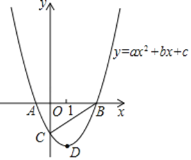��Ŀ����
����Ŀ����ͼ1��������![]() ��
��![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ������
������![]() �ı�
�ı�![]() ���ӳ�
���ӳ�![]() ���������ڵ�
���������ڵ�![]() .
.
��1���������ߵı���ʽ��
��2����ͼ2����![]() ��ֱ��
��ֱ��![]() �Ϸ��������ϵ�һ�����㣬����
�Ϸ��������ϵ�һ�����㣬����![]() ��
��![]() ���ƽ���߽�ֱ��
���ƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ������Ϊ
������Ϊ![]() .��
.��![]() �ij�Ϊ
�ij�Ϊ![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵ�ǣ�����д��
�ĺ�����ϵ�ǣ�����д��![]() ��ȡֵ��Χ���������
��ȡֵ��Χ���������![]() �����ֵ��
�����ֵ��
��3�������![]() �������߶Գ����ϵ�һ�㣬���������Ƿ���ڵ�
�������߶Գ����ϵ�һ�㣬���������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����������������
Ϊ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����������������![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.

���𰸡���1�������߽���ʽΪy=��![]() x2��
x2��![]() x+2����2��l=��
x+2����2��l=��![]() ��m+
��m+![]() ��2+
��2+![]() �����ֵΪ
�����ֵΪ![]() ����3����2����
����3����2����![]() ����4����
����4����![]() ����2��2����
����2��2����
��������
�����������1�������������A��B�����꣬���ô���ϵ��������������߽���ʽ��
��2���������E�����꣬�Ӷ������ֱ��OE����ʽ����֪��PGH=45�㣬��m�ɱ�ʾ��PG�ij����Ӷ��ɱ�ʾ��l�ij��������ö��κ��������ʿ���������ֵ��
��3����ACΪ�ߺ�ACΪ�Խ��ߣ���ACΪ��ʱ����M���Գ���Ĵ��ߣ�����ΪF�����֤����MFN�ա�AOC�������M���Գ���ľ��룬�Ӷ������M��ĺ����꣬�����M������ꣻ��ACΪ�Խ���ʱ����AC���е�ΪK�������K�ĺ����꣬�Ӷ������M�ĺ����꣬���������߽���ʽ�����M�����꣮
�����������1��������OBDC�ı�CD=1��
��OB=1��
��AB=4��
��OA=3��
��A����3��0����B��1��0����
��A��B����������������߽���ʽ�ɵ�
![]() ��
��
���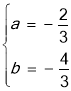 ��
��
�������߽���ʽΪy=��![]() x2��
x2��![]() x+2��
x+2��
��2����y=��![]() x2��
x2��![]() x+2�У���y=2�ɵ�2=��
x+2�У���y=2�ɵ�2=��![]() x2��
x2��![]() x+2�����x=0��x=��2��
x+2�����x=0��x=��2��
��E����2��2����
��ֱ��OE����ʽΪy=��x��
������ɵ�P��m����![]() m2��
m2��![]() m+2����
m+2����
��PG��y�ᣬ
��G��m����m����
��P��ֱ��OE���Ϸ���
��PG=��![]() m2��
m2��![]() m+2������m��=��
m+2������m��=��![]() m2��
m2��![]() m+2=��
m+2=��![]() ��m+
��m+![]() ��2+
��2+![]() ��
��
��ֱ��OE����ʽΪy=��x��
���PGH=��COE=45�㣬
��l=![]() PG=
PG=![]() [��
[��![]() ��m+
��m+![]() ��2+
��2+![]() ]=��
]=��![]() ��m+
��m+![]() ��2+
��2+![]() ��
��
����m=��![]() ʱ��l�����ֵ�����ֵΪ
ʱ��l�����ֵ�����ֵΪ![]() ��
��
��3������ACΪƽ���ı��εı�ʱ������MN��AC����MN=AC����ͼ����M���Գ���Ĵ��ߣ�����ΪF����AC���Գ����ڵ�L��
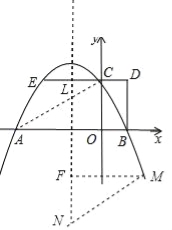
����ALF=��ACO=��FNM��
����MFN����AOC��
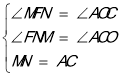
���MFN�ա�AOC��AAS����
��MF=AO=3��
����M���Գ���ľ���Ϊ3��
��y=��![]() x2��
x2��![]() x+2��
x+2��
�������߶Գ���Ϊx=��1��
��M��������x��y������|x+1|=3�����x=2��x=��4��
��x=2ʱ��y=��![]() ����x=��4ʱ��y=
����x=��4ʱ��y=![]() ��
��
��M��������2����![]() ����4����
����4����![]() ����
����
����ACΪ�Խ���ʱ����AC���е�ΪK��
��A����3��0����C��0��2����
��K����![]() ��1����
��1����
����N�ڶԳ����ϣ�
����N�ĺ�����Ϊ��1��
��M�������Ϊx��
��x+����1��=2������![]() ��=��3�����x=��2����ʱy=2��
��=��3�����x=��2����ʱy=2��
��M����2��2����
���Ͽ�֪��M������Ϊ��2����![]() ����4����
����4����![]() ����2��2����
����2��2����