题目内容
【题目】已知菱形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.

(1)若![]() ,求证:四边形
,求证:四边形![]() 是正方形
是正方形
(2)已知![]() ,求
,求![]() 的长;
的长;
(3)若![]() 固定,设
固定,设![]() ,将
,将![]() 绕着点
绕着点![]() 从点
从点![]() 开始逆时针旋转过程中,菱形
开始逆时针旋转过程中,菱形![]() 也随之变化,且
也随之变化,且![]() 满足
满足![]() ,若
,若![]() 是直角三角形,直接写出
是直角三角形,直接写出![]() 的值;
的值;
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由菱形的性质可得![]() ,由垂直平分线的性质可得,
,由垂直平分线的性质可得,![]() ,由等边对等角可得:
,由等边对等角可得:![]() ,等量代换可得
,等量代换可得![]() ,由平行线的判定及性质可得
,由平行线的判定及性质可得![]() ,
,![]() =90°,继而由正方形的判定求证结论;
=90°,继而由正方形的判定求证结论;
(2)由菱形的性质可知,![]() ,由相似三角形的判定可得
,由相似三角形的判定可得![]() ,继而由相似三角形对应边成比例的性质可得:
,继而由相似三角形对应边成比例的性质可得:![]() ,根据题(1)可知
,根据题(1)可知![]() ,进而可证△BGE∽△BAD,由此可知
,进而可证△BGE∽△BAD,由此可知![]() ,代入数据,求出
,代入数据,求出![]() ,最后由线段垂直平分线的性质求解;
,最后由线段垂直平分线的性质求解;
(3)根据题意,从旋转过程中可看出,线段![]() 在旋转360°的过程中,
在旋转360°的过程中,![]() 由0°增大到90°再减小到0°再增加到90°再到0°,据此结合图形即可求解.
由0°增大到90°再减小到0°再增加到90°再到0°,据此结合图形即可求解.
解:(1)∵四边形![]() 是菱形
是菱形
∴![]() ,∴
,∴![]() ,∵
,∵![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]()
∴![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ∴
∴![]() ∵
∵![]() ,
,
∴![]() ∵四边形
∵四边形![]() 是菱形
是菱形
∴四边形![]() 是正方形
是正方形
(2)∵四边形![]() 是菱形
是菱形
∴![]() ,∴
,∴![]() ;
;
∴![]() ∴
∴![]()
∵![]() ∴△BGE∽△BAD,∴
∴△BGE∽△BAD,∴![]()
∵![]() ∴
∴![]()
∵![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ∴
∴![]() .
.
(3)若![]() 是直角三角形时
是直角三角形时![]() 的值可能是60°,90°,270°或300°
的值可能是60°,90°,270°或300°
∵从旋转过程中可看出,线段![]() 在旋转360°的过程中,
在旋转360°的过程中,![]() 由0°增大到90°再减小到0°再增加到90°再到0°
由0°增大到90°再减小到0°再增加到90°再到0°
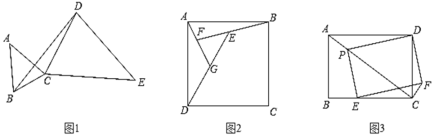
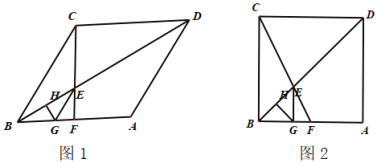
∴第一次出现![]() 是直角三角形时,如图1所示,此时
是直角三角形时,如图1所示,此时![]() 为
为![]() 的一半,可得旋转角度
的一半,可得旋转角度![]() 即
即![]() 为60°;第二次出现
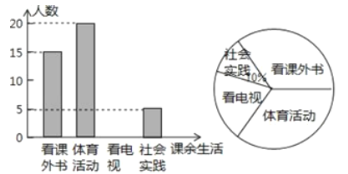
为60°;第二次出现![]() 是直角三角形时,如图2所示,此时(1)中已证明旋转角度
是直角三角形时,如图2所示,此时(1)中已证明旋转角度![]() 即
即![]() 为90°;当继续旋转时
为90°;当继续旋转时![]() 到达
到达![]() 的下方,同理可得旋转角度
的下方,同理可得旋转角度![]() 为270°和300°.
为270°和300°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目