题目内容
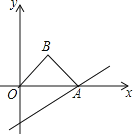
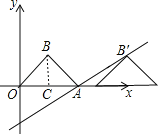
【题目】如图,直线y=![]() x﹣2与x轴交于点A,以OA为斜边在x轴的上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=
x﹣2与x轴交于点A,以OA为斜边在x轴的上方作等腰直角三角形OAB,将△OAB沿x轴向右平移,当点B落在直线y=![]() x﹣2上时,则线段AB在平移过程中扫过部分的图形面积为_____.
x﹣2上时,则线段AB在平移过程中扫过部分的图形面积为_____.
【答案】12.
【解析】
根据等腰直角三角形的性质求得点BC、OC的长度,即点B的纵坐标,表示出B′的坐标,代入函数解析式,即可求出平移的距离,进而根据平行四边形的面积公式即可求得.
y=![]() x﹣2,
x﹣2,
当y=0时,![]() x﹣2=0,
x﹣2=0,
解得:x=4,
即OA=4,
过B作BC⊥OA于C,
∵△OAB是以OA为斜边的等腰直角三角形,
∴BC=OC=AC=2,
即B点的坐标是(2,2),
设平移的距离为a,
则B点的对称点B′的坐标为(a+2,2),
代入y=![]() x﹣2得:2=
x﹣2得:2=![]() (a+2)﹣2,
(a+2)﹣2,
解得:a=6,
即△OAB平移的距离是6,
∴Rt△OAB扫过的面积为:6×2=12,
故答案为:12.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目