题目内容
【题目】如图,在每个小正方形的边长为1的网格中,A,B,D,E为格点,C为![]() ,
,![]() 的延长线的交点.
的延长线的交点.
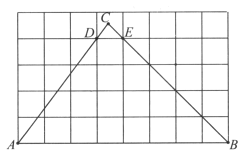
(Ⅰ)![]() 的结果为_________________.
的结果为_________________.
(Ⅱ)若点R在线段![]() 上,点S在线段
上,点S在线段![]() 上,点T在线段
上,点T在线段![]() 上,且满足四边形
上,且满足四边形![]() 为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形
为菱形,请在如图所示的网格中,用无刻度的直尺,画出菱形![]() ,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
,并简要说明点R,S,T的位置是如何找到的(不要求证明)____________________.
【答案】![]() ; 见解析;
; 见解析;
【解析】
(Ⅰ)根据题意利用![]() ,进行分析计算即可得出答案;
,进行分析计算即可得出答案;
(Ⅱ)根据题意利用菱形的性质即对角线互相垂直平分进行分析即可.
解:(Ⅰ)由题意可知![]() ,
,
故答案为:![]() ;
;
(Ⅱ)如图,取格点F,G,H,连接GH,连接AF分别交GH,BC于点O,S;取AC与网格线的交点为T,连接TO并延长交AB于点R.连接RS,ST得到四边形ARST即为所求.


练习册系列答案
相关题目
【题目】在“五四青年节”来临之际,某校举办了以“我的青春我做主”为主题的演讲比赛.并从参加比赛的学生中随机抽取部分学生的演讲成绩进行统计(等级记为![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :一般,
:一般,![]() :较差),并制作了如下统计图表(部分信息未给出).
:较差),并制作了如下统计图表(部分信息未给出).
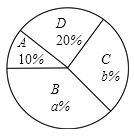
等级 | 人数 |
|
|
| 20 |
|
|
| 10 |
请根据统计图表中的信息解答下列问题:
(1)这次共抽取了______名参加演讲比赛的学生,统汁图中![]() ________,
________,![]() _______;
_______;
(2)求扇形统计图中演讲成绩等级为“一般”所对应扇形的圆心角的度数;
(3)若该校学生共2000人,如果都参加了演讲比赛,请你估计成绩达到优秀的学生有多少人?
(4)若演讲比赛成绩为![]() 等级的学生中恰好有2名女生,其余的学生为男生,从
等级的学生中恰好有2名女生,其余的学生为男生,从![]() 等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.
等级的学生中抽取两名同学参加全市演讲比赛,请用列表或画树状图的方法求出“恰好抽中—名男生和一名女生”的概率.



