ƒøƒ⁄»ð
°æƒø°øŒ ±≥æ∞£∫
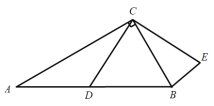
£®1£©»ÁÕº1£¨‘⁄°˜ABC∫Õ°˜CDE÷–£¨AB£ΩAC£¨EC£ΩED£¨°œBAC£Ω°œCED£¨«Î‘⁄Õº÷–◊˜≥ˆ”ΰ˜BCDœýÀ∆µƒ»˝Ω«–Œ£Æ
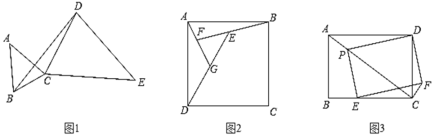
«®“∆”¶”√£∫
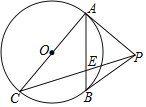
£®2£©»ÁÕº2£¨EŒ™’˝∑Ω–ŒABCDƒ⁄“ªµ„£¨°œDEB£Ω135°„£¨‘⁄DE…œ»°“ªµ„G£¨ πµ√BE£ΩEG£¨—”≥§BEΩªAG”⁄µ„F£¨«ÛAF£∫FGµƒ÷µ£Æ
¡™œµÕÿ’π£∫
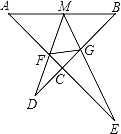
£®3£©æÿ–ŒABCD÷–£¨AB£Ω6£¨AD£Ω8£¨P°¢E∑÷± «AC°¢BC…œµƒµ„£¨«“Àƒ±þ–ŒPEFDŒ™æÿ–Œ£¨»Ù°˜PCD «µ»—¸»˝Ω«–Œ ±£¨÷±Ω”–¥≥ˆCFµƒ≥§£Æ
°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©![]() £ª£®3£©CF£Ω3ªÚ
£ª£®3£©CF£Ω3ªÚ![]() ªÚ
ªÚ![]() £Æ
£Æ
°æΩ‚Œˆ°ø
(1)»ÁÕº1÷–£¨¡¨Ω”AE£Æ‘Ú°˜ACE°◊°˜BCD£Æœ»÷§√˜°˜BAC°◊°˜DEC£¨Õ∆≥ˆ![]() £¨Ω‚戌 £ª
£¨Ω‚戌 £ª
(2)»ÁÕº2÷–£¨π˝D◊˜DM°ÕBFΩªBF—”≥§œþ”⁄M£¨¡¨AM£¨BD£¨œÎ∞Ï∑®÷§√˜°˜AMF°´°˜EGF£¨ø…µ√![]() £Æ
£Æ
(3)◊˜DJ°ÕAC”⁄J£¨÷§√˜°˜ADP°◊°˜CDF£¨Õ∆≥ˆ![]() =
=![]() £¨ø…µ√CF=
£¨ø…µ√CF=![]() =
=![]() =
=![]() PA£¨∑÷»˝÷÷«È–Œ∑÷±«Û≥ˆPAº¥ø…Ω‚æˆŒ £Æ
PA£¨∑÷»˝÷÷«È–Œ∑÷±«Û≥ˆPAº¥ø…Ω‚æˆŒ £Æ
(1)»ÁÕº1÷–£¨¡¨Ω”AE£Æ‘Ú°˜ACE°◊°˜BCD£Æ
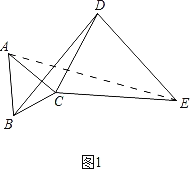
¿Ì”…£∫°þ‘⁄°˜ABC∫Õ°˜CDE÷–£¨AB=AC£¨EC=ED£¨°œBAC=°œCED£¨
°ý![]() =
=![]() £¨
£¨
°ý°˜BAC°◊°˜DEC£¨
°ý![]() £¨
£¨
°þAB=AC£¨EC=ED£¨°œBAC=°œCED£¨
°ý°œACB=°œABC=°œDCE=°œEDC£¨
°ý°œACE=°œBCD£¨
°ý°˜ACE°◊°˜BCD£ª
(2)»ÁÕº2÷–£¨π˝D◊˜DM°ÕBFΩªBF—”≥§œþ”⁄M£¨¡¨AM£¨BD£¨
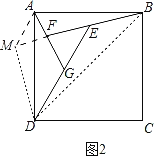
°þ°œBED=135°„£¨
°ý°œMED=45°„
°ý°˜MEDŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
”…’˝∑Ω–ŒABCDø…÷™°˜ADBŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ý![]() £¨º¥
£¨º¥![]() £¨
£¨
”÷°œMDE=°œADB=45°„£¨
°ý°œMDA=°œEDB£¨
°ý°˜AMD°´°˜BED£¨
°ý°œAMD=°œBED=135°„£¨«“![]() £¨
£¨
°ý°œAMF=°œFEG=45°„£¨
°ýAM°ŒED£¨
°ý°˜AMF°´°˜EGF£¨
![]() £ª
£ª
(3)»ÁÕº3÷–£¨◊˜DJ°ÕAC”⁄J£Æ
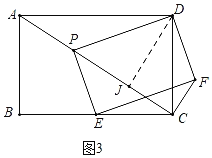
°þÀƒ±þ–ŒABCD «æÿ–Œ£¨
°ý°œADC=°œBCD=90°„£¨AD=BC=8£¨AB=CD=6£¨
°ýAC=![]() =
=![]() =10£¨
=10£¨
°þS°˜ADC=![]() ADDC=
ADDC=![]() ACDJ£¨
ACDJ£¨
°ýDJ=![]() =
=![]() £¨
£¨
°þÀƒ±þ–ŒDPEF «æÿ–Œ£¨
°ý°œECD=°œEFD=90°„£¨
°ýE£¨C£¨F£¨DÀƒµ„π≤‘≤£¨
°þE£¨F£¨D£¨PÀƒµ„π≤‘≤£¨
°ýE£¨C£¨F£¨D£¨PŒÂµ„π≤‘≤£¨
°ý°œPCF=°œPEF=90°„£¨
°ý°œBCD=°œPCF=90°„£¨
°ý°œACB=°œDCF£¨
°þAD°ŒBC£¨
°ý°œDAC=°œACB£¨
°ý°œDAP=°œDCF£¨
°þ°œADC=°œPDF=90°„£¨
°ý°œADP=°œCDF£¨
°ý°˜ADP°◊°˜CDF£¨
°ý![]() =
=![]() £¨
£¨
°ýCF=![]() =
=![]() =
=![]() PA£¨
PA£¨
¢Ÿµ±DP=DC ±£¨
°þDJ°ÕPC£¨
°ýCJ=PJ=![]() =
= =
=![]() £¨
£¨
°ýPA=10©Å![]() =
=![]() £¨
£¨
°ýCF=![]() °¡
°¡![]() =
=![]() £ª
£ª
¢⁄µ±CD=CP=6 ±£¨PA=10©Å6=4£¨CF=![]() °¡4=3£Æ
°¡4=3£Æ
¢€µ±PD=PC ±£¨PA=PC=PD=5£¨
°ýCF=![]() °¡5=
°¡5=![]() £¨
£¨
◊€…œÀ˘ ˆ£¨CF=3ªÚ![]() ªÚ
ªÚ![]()