题目内容
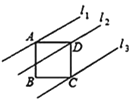
【题目】如图，直线l1，l2，l3分别过正方形ABCD的三个顶点A，D，C，且相互平行，若l1，l2的距离为2，l2，l3的距离为4，则正方形的对角线长为_______________．
【答案】
【解析】
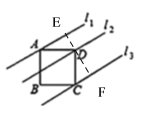
过D点作EF垂直l3于F点.利用一线三等角的模型证明△ADE△DCF，即可求出AE的长，用勾股定理求出正方形的边长及对角线长即可.
过D点作EF⊥l3于F点.
∵l1∥l2∥l3
∴EF⊥l1，EF⊥ l2
∴∠AED=∠DFC=90°，
∵四边形ABCD是正方形
∴∠ADC=90°,AD=CD
∴∠ADE+∠CDF=90°，∠ADE+∠EAD=90°
∴∠CDF=∠EAD
∴△ADE△DCF（AAS）
∴AE=DF
∵l1，l2的距离为2，l2，l3的距离为4，
∴AE=DF=4，ED=2
根据勾股定理得，AD=
∴正方形的对角线长为=
故答案为：
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
