Question

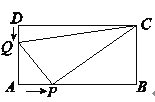
【题目】如图，在四边形ABCD中，AB＝BC＝CD＝AD＝4，∠DAB＝∠B＝∠C＝∠D＝90°，E，F分别是边BC，CD上的点，且CE＝BC，F为CD的中点，问△AEF是什么三角形？请说明理由.

Answer 1

【答案】直角三角形,理由见解析

【解析】

根据CE＝BC，F为CD的中点，求出CE、CF、DF、BE的长，利用勾股定理求出EF2、AF2、AE2的长，利用勾股定理的逆定理判定即可.

∵AB＝BC＝CD＝AD＝4，CE＝BC，F为CD的中点

∴CE=1,CF=DF=2,BE=3

又∵∠DAB＝∠B＝∠C＝∠D＝90°

∴EF2=CE2+CF2=12+22=5 ,AF2=AD2+DF2=22+42=20 ,AE2=AB2+BE2=42+32=25

∵EF2+ AF2=5+20=25 =AE2

∴△AEF是直角三角形.