题目内容
【题目】已知：
，点
是平面上一点，射线
与直线
交于点
，射线
与直线
交于点
，过点
作
，
与
所在的直线交于点
.
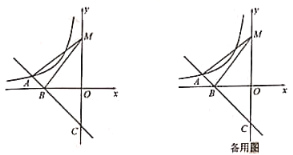
（1）如图1，当
，
时，写出
的一个余角，并证明
；
（2）若
，
.
①如图2，当点在内部时，用等式表示
与
之间的数量关系，并加以证明；
②如图3，当点在外部时，依题意补全图形，并直接写出用等式表示的与之间的数量关系.
【答案】（1）∠ADB等；（2）①
，证明见解析；②
【解析】
（1）根据余角的定义写出即可；根据同角的余角相等证明
，再由平行线的性质证明
，从而得出结论；
（2）①由
是
的外角可得
，
是
的外角，得
，再证明
，进行代入求值即可得出结论；
②方法同①.
（1）如图3
的余角不唯一，如
，写出一个即可.
证明：∵
∴
，
∴
∵
∴
∴
（2）
证明，如图4
∵是的外角
∴
∵是的外角
∴
∵
∴
∴
∵
∴
∴
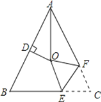
②补全图形见图5，
∵AF∥FC，
∴∠CAF=∠ACE
∵∠AEM是△ACE的外角
∴∠AEM=∠ACE+∠BAC，
∵∠AEM是△BME的外角
∴∠AEM=∠BME+∠MBE，
∴∠BME+∠MBE =∠ACE+∠BAC
∵
，
∴120°+∠MBE =∠ACE+80°
∴
∴
练习册系列答案
相关题目
