题目内容
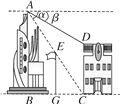
【题目】如图，在两建筑物之间有一根高15米的旗杆，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°.若旗杆底点G为BC的中点，则矮建筑物的高CD为( )
A. 20米 B. 10
米 C. 15
米 D. 5
米
【答案】A
【解析】如图所示，AC交旗杆于点E，延长CD至F，则DF⊥AF.
由题可知，∠ABC=∠EGC=90°，
又∵∠C=∠C，
∴△ABC∽△EGC.
∵G是BC的中点，
∴AB=2GE=30m.
在Rt△ABC中，BC=AB·tan∠BAC=AB·tan（90°-α）=10
m.
又在Rt△ADF中，AF=BC=10
，DF=AF·tanβ=10m.
所以矮建筑物的高度CD=FC-FD=AB-FD=30-10=20m.
故选A.
练习册系列答案
相关题目
